Classification En Groupes Emboités Collège Exercices

Salut ! On se retrouve pour parler maths, mais pas n'importe quelles maths. Celles qui, souvent, font froncer les sourcils au collège : la classification en groupes emboîtés. C'est un sujet qui peut paraître compliqué au premier abord, n'est-ce pas ? Mais promis, on va décortiquer ça ensemble, tranquillement, comme si on partageait un bon café.

Imagine. Tu as une boîte pleine de choses. Des jouets, des billes, des cartes... Tout mélangé ! Et tu dois ranger tout ça de manière logique. C'est un peu le principe de la classification. On prend un ensemble d'éléments et on les range dans des catégories. Simple, non ?

Qu'est-ce que la Classification en Groupes Emboîtés ?

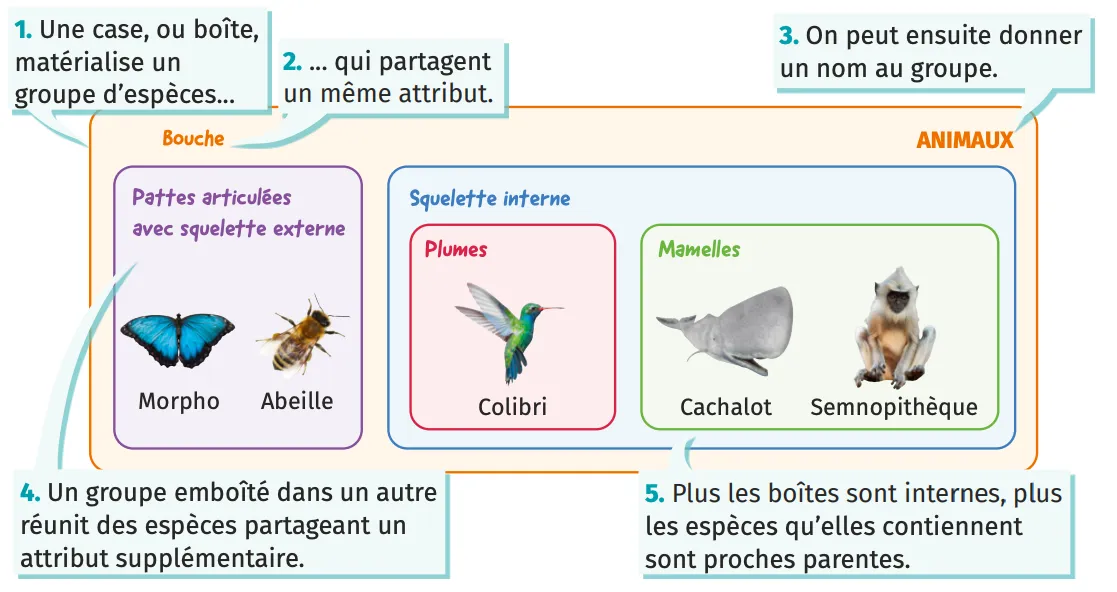
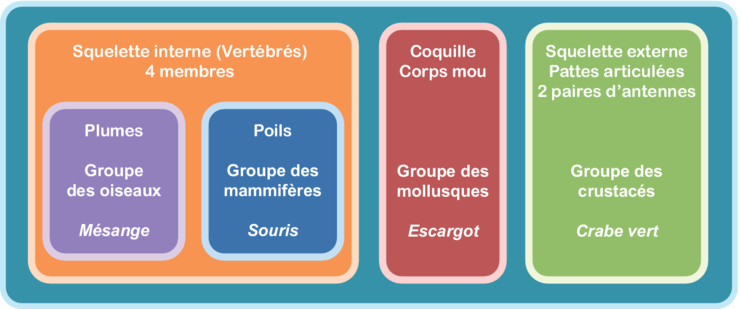
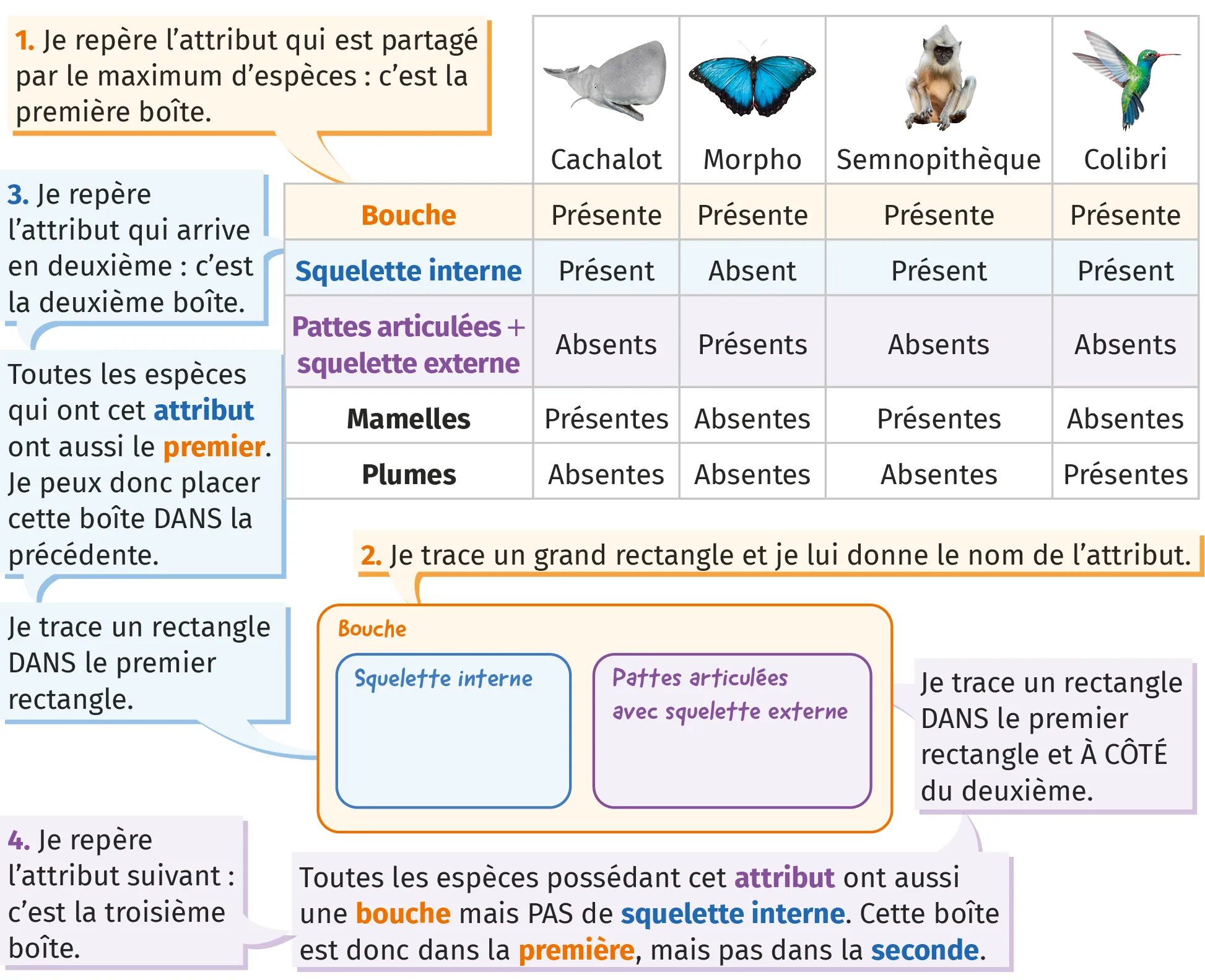
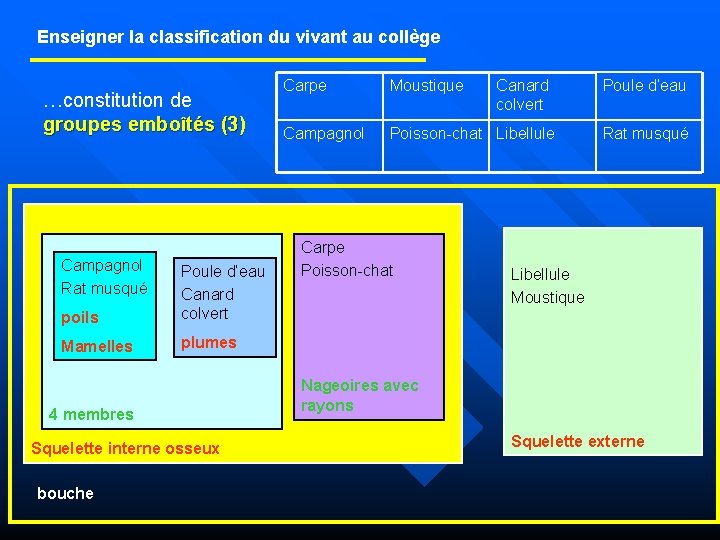
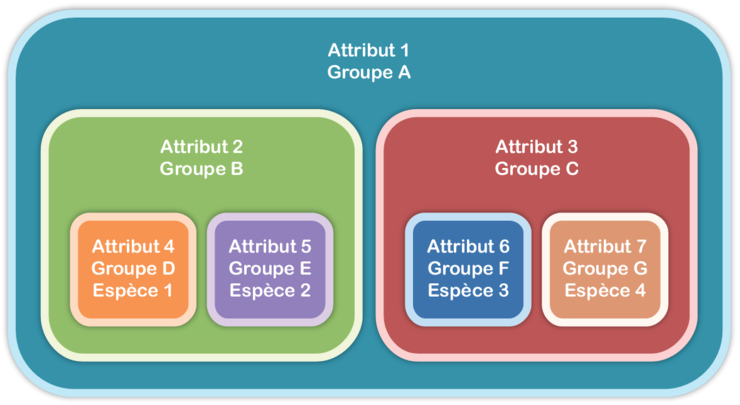
Alors, les groupes emboîtés, c'est quoi exactement ? Imagine des poupées russes. Une grande poupée, à l'intérieur une plus petite, et ainsi de suite. Chaque poupée est un groupe. La petite poupée est *contenue* dans la plus grande. C'est ça, l'idée ! Un groupe est inclus dans un autre, qui est lui-même inclus dans un autre, et ainsi de suite. On parle d'inclusion. C'est un concept clé.

En maths, ça se traduit comment ? Prenons un exemple simple : les nombres. On a les nombres entiers naturels (0, 1, 2, 3...). Puis, on a les nombres entiers relatifs (..., -2, -1, 0, 1, 2...). On voit bien que tous les nombres entiers naturels sont aussi des nombres entiers relatifs. Les entiers naturels sont *emboîtés* dans les entiers relatifs. C’est clair, ça ?

On peut aller plus loin. Ensuite, on a les nombres rationnels (les fractions, comme 1/2, 3/4, -5/7). Et puis les nombres réels (tous les nombres que l'on peut imaginer sur une droite numérique, y compris les nombres irrationnels comme π ou √2). Et enfin, les nombres complexes (qui font intervenir le fameux "i", la racine carrée de -1). Vous suivez toujours ?

Ainsi, on a une classification en groupes emboîtés :

• Nombres entiers naturels ⊆ Nombres entiers relatifs ⊆ Nombres rationnels ⊆ Nombres réels ⊆ Nombres complexes

Le symbole ⊆ signifie "est inclus dans". C'est important de le retenir !

Pourquoi c'est important au collège ?

Bon, vous vous demandez peut-être : "Ok, c'est joli tout ça, mais à quoi ça sert concrètement au collège ?" Excellente question !

Comprendre les groupes emboîtés, ça aide à mieux comprendre les propriétés des nombres. Par exemple, si on sait qu'un nombre est entier naturel, on sait automatiquement qu'il est aussi entier relatif, rationnel, réel et complexe. Ça évite de se poser 10 000 questions à chaque fois !

Ça permet aussi de simplifier les raisonnements et de mieux résoudre les exercices. Et oui, c'est ça le but final : devenir un pro des maths !

Exercices Concrets : On se Lance !

Allez, on passe aux choses sérieuses. Voici quelques types d'exercices que vous pouvez rencontrer au collège sur la classification en groupes emboîtés :

• Identifier à quel ensemble de nombres appartient un nombre donné. Par exemple, 3/7 est-il un nombre entier ? Un nombre rationnel ? Un nombre réel ?
• Vrai ou faux : Affirmer si une proposition est vraie ou fausse. Par exemple, "Tous les nombres entiers relatifs sont des nombres entiers naturels" (faux !) ou "Tous les nombres rationnels sont des nombres réels" (vrai !).
• Démonstration simple. Par exemple, prouver que si un nombre est un entier pair, alors il est aussi un nombre rationnel.
• Résolution de problèmes. Des petits problèmes où la compréhension des ensembles de nombres est cruciale.

Prenons un exemple d'exercice. On vous donne le nombre -5. À quels ensembles de nombres appartient-il ?

Réponse :

• Il n'est pas un nombre entier naturel (car les entiers naturels sont positifs ou nuls).
• C'est un nombre entier relatif (car il est un entier négatif).
• C'est un nombre rationnel (car on peut l'écrire sous forme de fraction : -5/1).
• C'est un nombre réel (car il peut être placé sur une droite numérique).
• C'est un nombre complexe (car tous les nombres réels sont aussi des nombres complexes).

Voilà ! Pas si compliqué, n'est-ce pas ?

Conseils et Astuces

Pour bien maîtriser la classification en groupes emboîtés, voici quelques conseils :

• Apprenez bien les définitions de chaque ensemble de nombres. C'est la base.
• Faites des exercices, beaucoup d'exercices ! C'est en pratiquant qu'on devient bon.
• Visualisez les ensembles. Imaginez des cercles qui s'emboîtent les uns dans les autres.
• N'hésitez pas à demander de l'aide à votre professeur ou à vos camarades si vous bloquez.
• Amusez-vous ! Les maths, ça peut être amusant, si on aborde ça avec le bon état d'esprit.

Et surtout, ne vous découragez pas ! La classification en groupes emboîtés, ça demande un peu de temps et de pratique, mais avec de la persévérance, vous finirez par maîtriser ce sujet sur le bout des doigts. Et puis, avouons-le, c'est quand même assez satisfaisant de comprendre quelque chose qui paraissait compliqué au début, non ?

Alors, prêt à relever le défi ? Je suis sûr que oui ! Prenez votre cahier, votre stylo, et lancez-vous. Et souvenez-vous, les maths, c'est comme un jeu : plus on joue, plus on devient fort.

Voilà, notre petite pause mathématique touche à sa fin. J'espère que cet article vous a aidé à y voir plus clair sur la classification en groupes emboîtés. À bientôt pour de nouvelles aventures mathématiques ! Et n'oubliez pas : les maths, c'est l'aventure de l'esprit !