Comment Trouver Le Maximum Et Le Minimum D'une Fonction

Salut l'ami(e) ! Alors, on papote maths aujourd'hui ? Plus précisément, comment dénicher les maxima et minima d'une fonction ? Pas de panique, c'est moins effrayant qu'il n'y paraît. Promis ! On va décortiquer ça ensemble, café à la main (ou thé, si tu préfères, on ne juge pas !).

En gros, trouver le maximum et le minimum d'une fonction, c'est comme chercher le point le plus haut et le point le plus bas sur une montagne russe. Imagine : tu es dans un wagon, et tu veux savoir à quelle hauteur tu vas crier le plus fort (le maximum), et à quel moment tu auras le plus envie de fermer les yeux (le minimum). Fun, non ?

L'Art de la Dérivée : Notre Outil Secret

La dérivée, c'est notre arme secrète. Oui, oui, la même dérivée qui te donnait des sueurs froides au lycée. Mais attendez ! Elle est là pour nous aider, pas pour nous torturer. La dérivée, c'est un peu comme un détecteur de pente. Elle nous dit si la fonction monte, descend, ou est plate (comme une crêpe !).

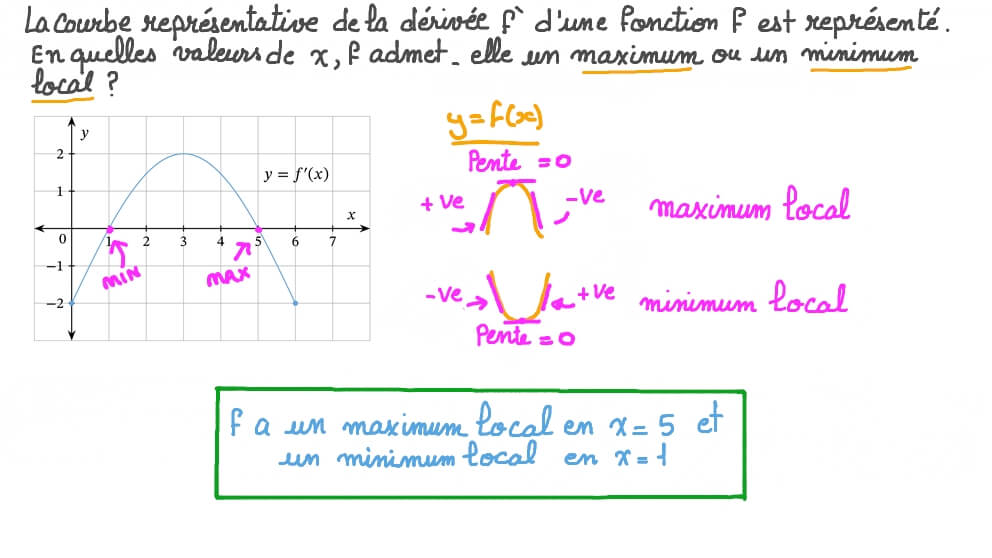
Et pourquoi la pente est-elle importante ? Parce que aux points les plus hauts (maxima) et les plus bas (minima), la pente est… zéro ! Eureka ! Enfin, pas toujours, mais on y reviendra. Disons que c'est un bon point de départ.

Étape 1 : Calculer la Dérivée (Respirez profondément !)

On commence par dériver notre fonction. Je sais, je sais, certains ont des souvenirs douloureux de cette étape. Mais il existe plein de calculateurs en ligne si tu as la flemme de le faire à la main. On est au 21ème siècle, profitons-en !

Prenons un exemple simple : f(x) = x² - 4x + 3. La dérivée, c'est f'(x) = 2x - 4. Voilà, c'est fait ! Pas si terrible, hein ? Tu vois, tu es capable de tout !

Étape 2 : Trouver les Points Critiques (Là où la Magie Opère)

Maintenant, on doit trouver les points critiques. Ce sont les points où la dérivée est égale à zéro, ou bien n'existe pas. Ces points critiques sont les suspects potentiels pour nos maxima et minima.

Pour notre exemple, on pose f'(x) = 0, donc 2x - 4 = 0. Ce qui nous donne x = 2. Bingo ! x = 2 est notre unique suspect pour l'instant.

Attends, "n'existe pas" ? Oui, certaines fonctions ont des dérivées qui ne sont pas définies en certains points (par exemple, une division par zéro). Ces points sont aussi des points critiques à examiner.

Étape 3 : Le Test de la Dérivée Seconde (ou le Test de la Première Dérivée)

On a trouvé nos suspects, mais comment savoir si x = 2 est un maximum, un minimum, ou... rien du tout ? C'est là que le test de la dérivée seconde entre en jeu. Ou, si on est un peu paresseux (ça arrive !), on peut utiliser le test de la première dérivée.

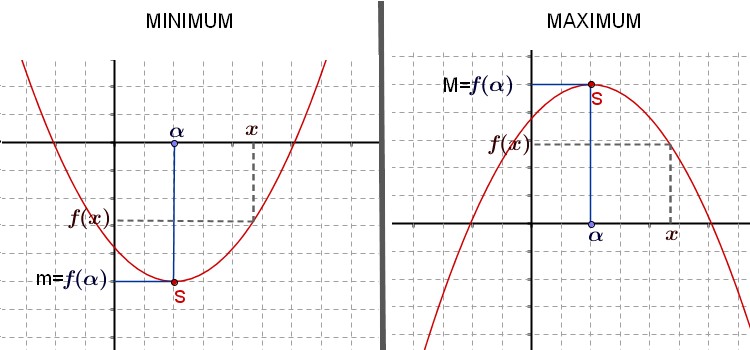
Test de la dérivée seconde : On calcule la dérivée seconde de f(x). Pour notre exemple, f''(x) = 2. On évalue la dérivée seconde au point critique x = 2. f''(2) = 2. Comme c'est positif, ça veut dire que la fonction est "heureuse" à ce point (elle a le sourire vers le haut). Donc, c'est un minimum ! Super !

Test de la première dérivée : On regarde le signe de la première dérivée avant et après le point critique. Si la dérivée passe de négative à positive, c'est un minimum. Si elle passe de positive à négative, c'est un maximum. Si elle ne change pas de signe, c'est un point d'inflexion (ni maximum, ni minimum).

Pour notre exemple, avant x = 2 (par exemple, à x = 1), f'(1) = -2 (négatif). Après x = 2 (par exemple, à x = 3), f'(3) = 2 (positif). Donc, ça confirme que x = 2 est un minimum !

Étape 4 : Calculer la Valeur du Minimum (ou du Maximum)

Maintenant qu'on sait que x = 2 est un minimum, on peut calculer la valeur de la fonction en ce point pour savoir à quelle hauteur se trouve ce minimum. On remplace x par 2 dans notre fonction originale : f(2) = 2² - 4(2) + 3 = 4 - 8 + 3 = -1. Donc, le minimum de la fonction est -1, et il est atteint en x = 2.

Attention aux Pièges ! (Les Chausse-Trappes Mathématiques)

Il y a quelques petits pièges à éviter :

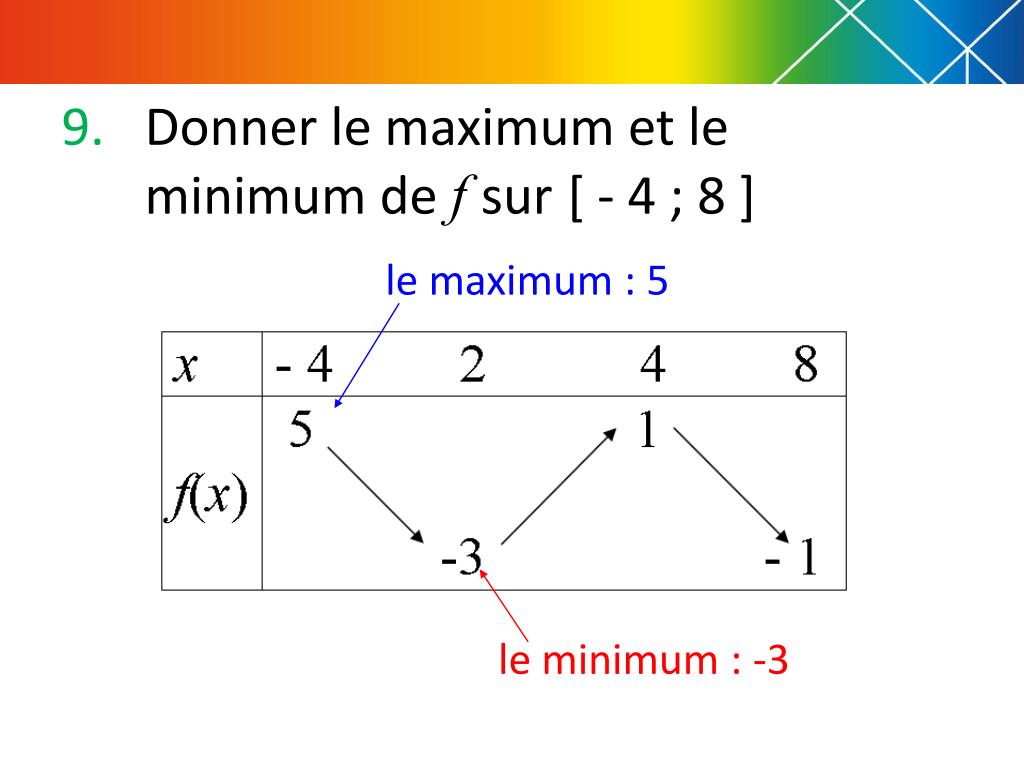
• Les bornes de l'intervalle : Si on cherche le maximum et le minimum d'une fonction sur un intervalle fermé (par exemple, entre 0 et 5), il faut aussi regarder les valeurs de la fonction aux bornes de l'intervalle. Le maximum ou le minimum peut se trouver là !
• Les points où la dérivée n'existe pas : On en a parlé, mais c'est important de s'en souvenir. Ces points peuvent être des extrema même si la dérivée est infinie ou indéfinie.
• Les points d'inflexion : Ce ne sont ni des maxima, ni des minima, mais ils peuvent ressembler à des extrema "paresseux". Fais attention !

Les Maxima et Minima Locaux vs. Globaux (Le Grand Jeu)

Il y a une distinction importante à faire entre les maxima et minima locaux et globaux.

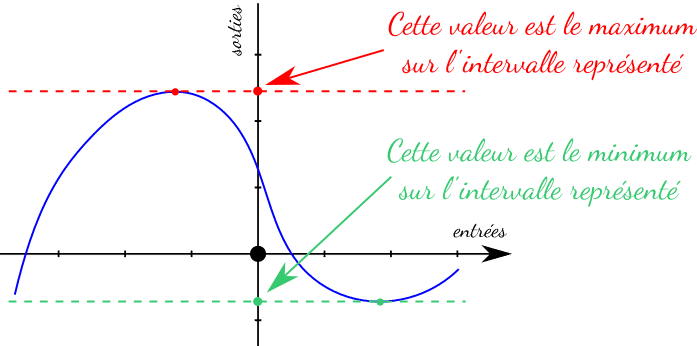
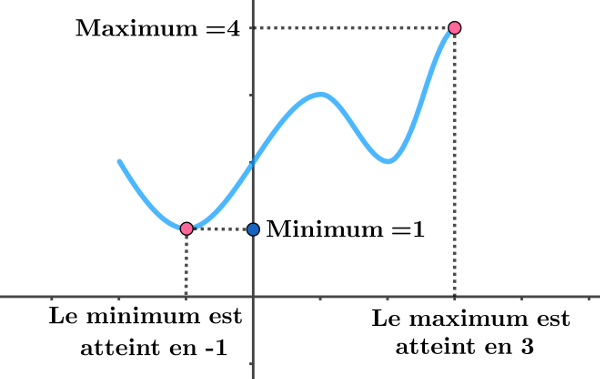
Un maximum local est un point qui est plus haut que tous les points qui l'entourent proche. Imagine le sommet d'une petite colline. Un minimum local, c'est pareil, mais en bas (le fond d'un petit creux).

Un maximum global (ou absolu) est le point le plus haut de toute la fonction. Un minimum global (ou absolu) est le point le plus bas. Imagine le sommet de l'Everest (maximum global) et le fond de la fosse des Mariannes (minimum global). Ils dominent tout le paysage !

Pour trouver le maximum et le minimum global, il faut comparer tous les maxima et minima locaux, et les valeurs aux bornes de l'intervalle (si on en a un). Celui qui est le plus haut est le maximum global, et celui qui est le plus bas est le minimum global. Simple, non ?

En Résumé (La Recette Gagnante)

Alors, comment trouver le maximum et le minimum d'une fonction, étape par étape ?

1. Dériver la fonction. (On respire, tout va bien se passer !)
2. Trouver les points critiques. (Là où la dérivée est zéro ou n'existe pas.)
3. Utiliser le test de la dérivée seconde (ou le test de la première dérivée) pour déterminer si chaque point critique est un maximum, un minimum, ou ni l'un ni l'autre.
4. Calculer la valeur de la fonction aux points critiques pour trouver la valeur des maxima et minima.
5. Si on a un intervalle, regarder les valeurs aux bornes.
6. Comparer tous les maxima et minima locaux, et les valeurs aux bornes, pour trouver le maximum et le minimum global.

Et voilà ! Tu es maintenant un expert en recherche de maxima et minima. Tu peux aller impressionner tes amis (ou les ennuyer, c'est selon). N'hésite pas à t'entraîner avec d'autres fonctions, et si tu as des questions, reviens me voir ! On prendra un autre café (ou thé) et on en reparlera. À bientôt !