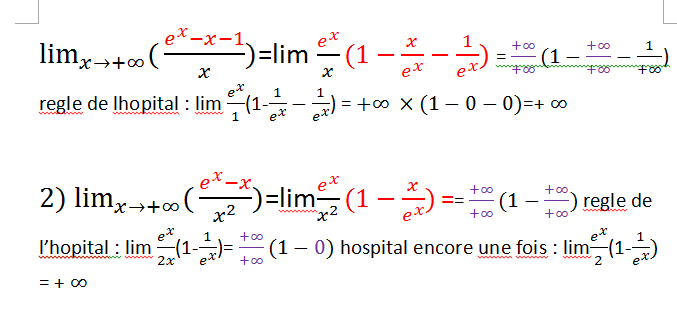Cours Limite De Fonction

Ah, les limites de fonctions… un sujet qui peut sembler intimidant au premier abord, n'est-ce pas ? Mais croyez-moi, c'est bien plus abordable qu'il n'y paraît. Imaginez que vous vous approchez d'une ligne d'horizon. Vous vous en rapprochez de plus en plus, mais vous ne la touchez jamais vraiment. C'est un peu ça, une limite !

Alors, on se lance ?

Qu'est-ce qu'une limite, au juste ?

En termes simples, la limite d'une fonction, disons f(x), lorsque x tend vers une certaine valeur, disons a, est la valeur vers laquelle f(x) se rapproche de plus en plus lorsque x se rapproche de a. Est-ce clair ? Pas de panique si ce n'est pas le cas, on va décortiquer tout ça ensemble !

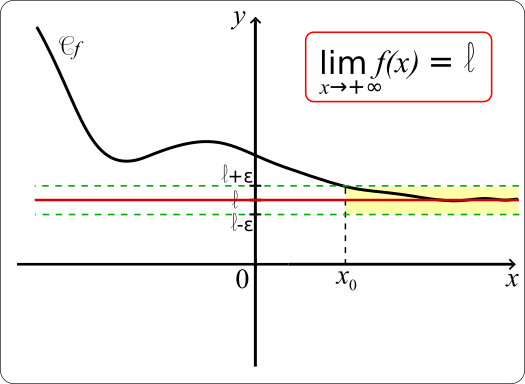
On note ça comme ceci : lim (x→a) f(x) = L. Ce qui se lit : "La limite de f(x) quand x tend vers a est égale à L".

Prenons un exemple tout simple : la fonction f(x) = x + 1. Si on veut savoir ce qui se passe quand x se rapproche de 2, eh bien, on voit que f(x) se rapproche de 3. Donc, lim (x→2) (x+1) = 3. Facile, non ?

Mais attention ! La limite n'est pas forcément la valeur de la fonction au point considéré. C'est là où ça devient intéressant !

Pourquoi s'embêter avec les limites ?

Bonne question ! Pourquoi se casser la tête avec ce concept abstrait ? Eh bien, les limites sont les fondations du calcul différentiel et intégral. Sans les limites, pas de dérivées, pas d'intégrales… bref, pas de maths "avancées" ! Elles sont cruciales pour comprendre la continuité, la convergence de suites et de séries, et bien d'autres concepts fondamentaux. Elles permettent aussi de gérer des situations où les fonctions se comportent de manière un peu bizarre, par exemple, quand elles tendent vers l'infini.

Imaginez, par exemple, que vous essayez de calculer la vitesse instantanée d'une voiture. Vous ne pouvez pas simplement diviser la distance parcourue par le temps écoulé, car cela vous donnerait la vitesse moyenne. Pour obtenir la vitesse instantanée, vous devez prendre une limite : vous faites tendre l'intervalle de temps vers zéro ! C'est la base du calcul différentiel.

Comment calculer une limite ?

Il existe plusieurs techniques pour calculer les limites. Certaines sont assez intuitives, d'autres un peu plus subtiles. Voici quelques approches courantes :

• Substitution directe : Si la fonction est continue au point considéré, vous pouvez simplement remplacer x par a dans l'expression de la fonction. C'est ce qu'on a fait dans notre exemple précédent avec f(x) = x + 1.
• Factorisation : Parfois, vous pouvez simplifier l'expression de la fonction en factorisant le numérateur et le dénominateur. Cela peut vous permettre d'éliminer des indéterminations.
• Multiplication par le conjugué : Si vous avez une expression avec une racine carrée, multiplier le numérateur et le dénominateur par le conjugué peut vous aider à simplifier l'expression.
• Règle de L'Hôpital : Cette règle est très utile pour calculer les limites de formes indéterminées comme 0/0 ou ∞/∞. Elle consiste à dériver le numérateur et le dénominateur jusqu'à ce que la limite devienne calculable. Mais attention, on ne peut pas l'appliquer à toutes les sauces !
• Théorème des gendarmes (ou théorème d'encadrement) : Si vous pouvez encadrer votre fonction entre deux autres fonctions dont les limites sont égales au point considéré, alors la limite de votre fonction est également égale à cette valeur.

Chaque technique a ses propres forces et faiblesses, et il est important de savoir quand utiliser chacune d'elles. La pratique est essentielle pour maîtriser ces techniques !

Les formes indéterminées : le mystère des limites

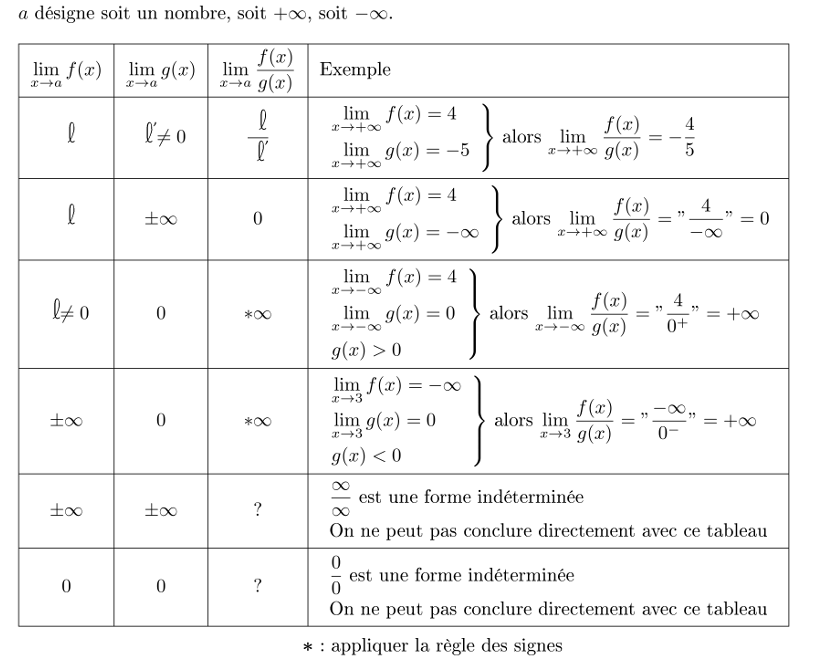
Ah, les formes indéterminées ! Ce sont ces expressions qui apparaissent lorsque vous essayez de calculer une limite par substitution directe et que vous obtenez quelque chose comme 0/0, ∞/∞, 0 * ∞, ∞ - ∞, 1^∞, 0⁰ ou ∞⁰. Ces expressions ne vous donnent pas directement la valeur de la limite. Elles vous indiquent simplement que vous devez utiliser une autre technique pour lever l'indétermination.

Par exemple, si vous avez lim (x→0) (sin(x)/x), vous obtenez 0/0 si vous substituez directement. C'est une forme indéterminée. Mais si vous appliquez la règle de L'Hôpital (en dérivant le numérateur et le dénominateur), vous obtenez lim (x→0) (cos(x)/1) = 1. Donc, la limite est 1.

Il est important de bien identifier les formes indéterminées et de savoir comment les lever. C'est un peu comme résoudre une énigme !

Les limites à l'infini

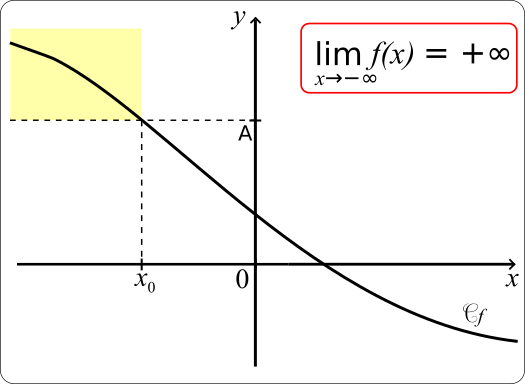
On peut aussi s'intéresser à ce qui se passe lorsque x tend vers l'infini (positif ou négatif). Cela peut nous donner des informations sur le comportement de la fonction "à long terme".

Par exemple, considérons la fonction f(x) = 1/x. Lorsque x devient de plus en plus grand (tend vers l'infini), f(x) se rapproche de plus en plus de zéro. Donc, lim (x→∞) (1/x) = 0. De même, lim (x→-∞) (1/x) = 0.

Les limites à l'infini sont utiles pour déterminer les asymptotes horizontales des fonctions. Une asymptote horizontale est une ligne horizontale à laquelle la courbe de la fonction se rapproche de plus en plus lorsque x tend vers l'infini (positif ou négatif).

Les limites à droite et à gauche

Parfois, la limite d'une fonction dépend de la direction par laquelle on s'approche du point considéré. On parle alors de limite à droite et de limite à gauche.

La limite à droite de f(x) en a, notée lim (x→a⁺) f(x), est la valeur vers laquelle f(x) se rapproche lorsque x se rapproche de a en étant supérieur à a.

La limite à gauche de f(x) en a, notée lim (x→a^-) f(x), est la valeur vers laquelle f(x) se rapproche lorsque x se rapproche de a en étant inférieur à a.

Pour que la limite de f(x) en a existe, il faut que la limite à droite et la limite à gauche existent et soient égales. Si ce n'est pas le cas, on dit que la limite n'existe pas.

Prenons l'exemple de la fonction f(x) = |x|/x. Pour x > 0, f(x) = 1, et pour x < 0, f(x) = -1. Donc, lim (x→0⁺) f(x) = 1 et lim (x→0^-) f(x) = -1. Comme les limites à droite et à gauche ne sont pas égales, la limite de f(x) en 0 n'existe pas.

Les limites à droite et à gauche sont particulièrement importantes pour étudier les fonctions définies par morceaux.

Voilà, on a fait un tour d'horizon des limites de fonctions. Ce n'est que le début de votre voyage dans le monde passionnant du calcul, mais j'espère que cela vous a donné une bonne base. N'oubliez pas : la clé est la pratique ! Alors, prenez votre courage à deux mains, faites quelques exercices, et vous verrez, les limites deviendront vos amies. Et rappelez-vous toujours que même les concepts les plus complexes peuvent être décomposés en étapes simples. Alors, respirez un bon coup et lancez-vous !