Dérivée De 2 Racine De X

Salut tout le monde ! Aujourd'hui, on va parler d'un truc qui sonne peut-être compliqué, mais qui est en réalité super cool : la dérivée de 2√x. Oui, oui, vous avez bien lu. On va décortiquer ça ensemble, promis, sans se prendre la tête ! Alors, prêt à embarquer dans le monde merveilleux des maths… enfin, un petit coin de ce monde ? Allons-y !

Pourquoi s'intéresser à ça ?

Vous vous demandez peut-être : "Mais pourquoi diable devrais-je m'intéresser à la dérivée de 2√x ? Ma vie est bien comme elle est, merci bien !". Et je vous comprends ! Mais en fait, les dérivées, c'est un peu comme avoir une loupe pour observer comment les choses changent. Imaginez que vous êtes sur une montagne russe. La dérivée, c'est ce qui vous permettrait de savoir à quelle vitesse vous montez ou descendez à chaque instant ! C'est puissant, non ? Et 2√x, c'est juste un exemple concret pour qu'on puisse s'amuser ensemble avec cette loupe.

Plus concrètement, les dérivées servent à plein de choses :

Optimisation : Trouver le meilleur moyen de faire quelque chose (maximiser des profits, minimiser des coûts, etc.).
Physique : Comprendre le mouvement des objets (vitesse, accélération).
Économie : Analyser les tendances du marché.
Informatique : Améliorer les algorithmes.

Alors, ça vous donne envie d'y jeter un coup d'œil, hein ? 😉

Comprendre les bases : Qu'est-ce qu'une dérivée ?

Avant de plonger dans le vif du sujet, rafraîchissons un peu les bases. Une dérivée, c'est en gros la pente d'une courbe en un point donné. Imaginez que vous dessinez une courbe sur un graphique. Si vous zoomez à fond sur un point de cette courbe, elle va ressembler à une ligne droite. La pente de cette ligne droite, c'est la dérivée en ce point. C'est aussi la vitesse à laquelle la fonction change à cet endroit précis.

Pour la calculer, on utilise une formule, mais pas de panique, on va la simplifier au maximum :

Si on a une fonction f(x), sa dérivée, notée f'(x), représente le taux de variation instantané de f(x) par rapport à x.

Ça semble barbare ? Pas tant que ça ! Pensez-y comme une recette de cuisine. On a des ingrédients (la fonction), une recette (la formule de dérivation) et à la fin, on obtient un plat délicieux (la dérivée) !

La dérivée de √x : Un petit détour avant d'attaquer le plat principal

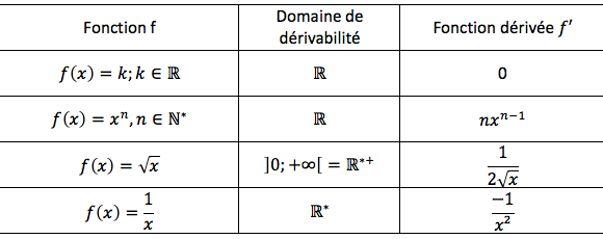
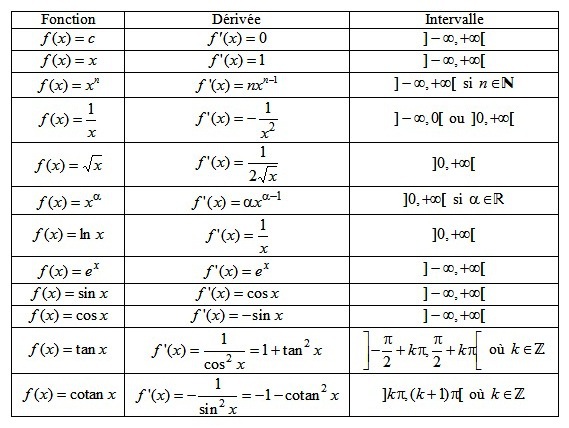
Avant de nous attaquer à 2√x, parlons de √x tout court. C'est un peu comme l'échauffement avant le grand match. La fonction √x, c'est la racine carrée de x. Graphiquement, elle ressemble à une demi-parabole couchée sur le côté. Sa dérivée, c'est 1/(2√x).

D'où ça sort, ce 1/(2√x) ? Eh bien, on utilise une règle de dérivation qu'on appelle la règle de la puissance. En gros, si on a xⁿ, sa dérivée c'est n*x^(n-1). Or, √x c'est la même chose que x^1/2. Donc, si on applique la règle de la puissance :

(1/2) * x^{(1/2 - 1)} = (1/2) * x^(-1/2) = 1 / (2√x)

Voilà ! On a fait le plus dur. Promis !

Enfin, la dérivée de 2√x !

Maintenant, le moment que vous attendiez tous (enfin, peut-être) : la dérivée de 2√x ! C'est là où les choses deviennent vraiment intéressantes. On a déjà vu que la dérivée de √x, c'est 1/(2√x). Mais on a un petit "2" devant la racine carrée. Qu'est-ce que ça change ?

Eh bien, c'est là qu'intervient une autre règle de dérivation : la règle du multiple constant. Cette règle nous dit que si on a une constante (un nombre) multipliée par une fonction, on peut simplement laisser la constante de côté et dériver la fonction. Ensuite, on multiplie le résultat par la constante. Facile, non ?

Donc, pour dériver 2√x, on fait comme ça :

On dérive √x, ce qui nous donne 1/(2√x).
On multiplie le résultat par 2 (la constante).

Ce qui nous donne : 2 * (1/(2√x)) = 1/√x

Et voilà ! La dérivée de 2√x, c'est 1/√x. C'est pas si compliqué finalement, hein ?

Un exemple concret pour bien comprendre

Imaginez que vous avez une fonction qui représente la distance parcourue par une fourmi en fonction du temps : d(t) = 2√t, où d(t) est la distance en centimètres et t est le temps en secondes. La dérivée de cette fonction, d'(t) = 1/√t, représente la vitesse de la fourmi à chaque instant. Par exemple, à t=1 seconde, la vitesse de la fourmi est de 1/√1 = 1 cm/s. À t=4 secondes, sa vitesse est de 1/√4 = 0.5 cm/s. On voit que la fourmi ralentit au fur et à mesure !

Pourquoi c'est cool, en résumé

Alors, pourquoi est-ce que tout ça est cool ? Parce que :

Ça nous permet de comprendre comment les choses changent.
Ça nous donne des outils pour optimiser des situations.
C'est une porte d'entrée vers des concepts mathématiques plus avancés.
Et surtout, parce que ça nous permet de briller en société (ou au moins d'impressionner nos amis 😉).

Plus sérieusement, comprendre les dérivées, même d'une fonction simple comme 2√x, c'est un peu comme apprendre à lire. Au début, on déchiffre les lettres une par une, mais ensuite, on peut lire des romans entiers et comprendre des histoires complexes. Les dérivées, c'est pareil. Au début, ça peut sembler abstrait, mais ensuite, on peut les utiliser pour résoudre des problèmes concrets et comprendre le monde qui nous entoure.

Et après ?

Si vous avez aimé cette petite exploration, n'hésitez pas à approfondir le sujet. Il existe plein de ressources en ligne, des vidéos, des cours, des exercices… Le monde des mathématiques est vaste et fascinant. Et n'oubliez pas, la clé, c'est la curiosité et la persévérance ! Alors, à vos calculs et à bientôt pour de nouvelles aventures mathématiques !