Encadrer Une Fraction Par Deux Nombres Entiers Consécutifs

Salut tout le monde ! Alors, vous vous êtes déjà demandé à quoi sert vraiment une fraction ? On les apprend à l'école, on les manipule, mais on a parfois du mal à voir leur utilité concrète. Eh bien, aujourd'hui, on va explorer une manière super pratique de les comprendre : en les encadrant par deux nombres entiers consécutifs. Accrochez-vous, ça va être plus fun que vous ne le pensez !

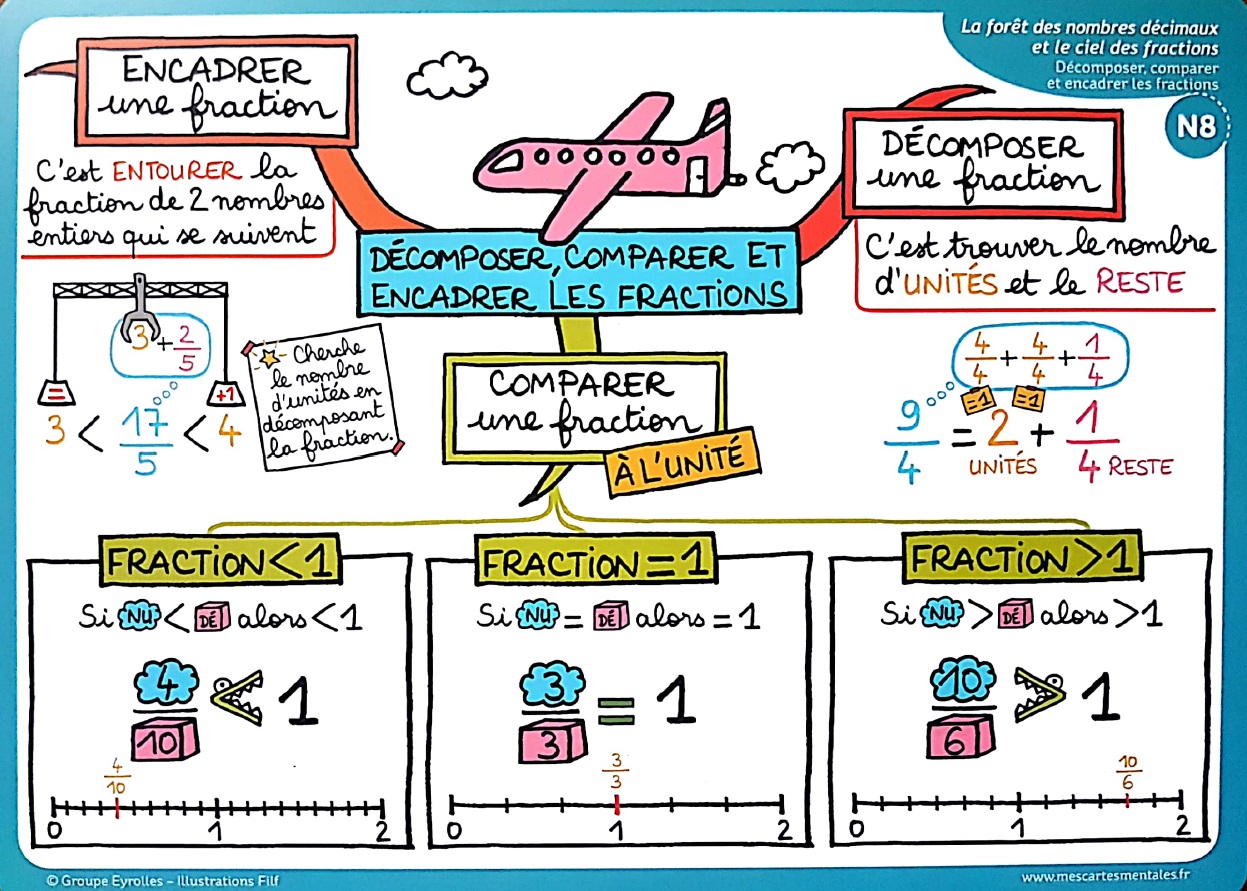
Pourquoi Encadrer une Fraction, C'est Cool ?

Encadrer une fraction par deux nombres entiers consécutifs, ça signifie trouver deux nombres entiers qui se suivent (comme 2 et 3, ou 10 et 11) de telle sorte que la fraction se situe entre ces deux nombres. Mais pourquoi faire ça ?

Imaginez que vous préparez une recette et qu'elle demande 3/4 de tasse de farine. Vous voyez tout de suite ce que ça représente, vous ? Peut-être pas instantanément. Mais si je vous dis que 3/4 est entre 0 et 1, là, vous visualisez déjà mieux : c'est moins qu'une tasse pleine, mais plus que rien du tout ! C'est ça, la magie de l'encadrement. Ça nous donne une idée claire de la taille de la fraction.

Visualiser Facilement

Pensez à une pizza. Si vous avez 5/8 de pizza, est-ce que c'est plus proche de la moitié de la pizza ou d'une pizza entière ? Si vous savez que 5/8 est entre 0 et 1, et même plus précisément entre 0 et 1/2 (la moitié) et 1, vous comprenez que vous avez moins qu'une pizza entière, un peu plus de la moitié. Encadrer, c'est un peu comme avoir un GPS pour les fractions !

• Estimation Rapide : Besoin d'estimer rapidement une quantité ? L'encadrement vous aide à vous faire une idée en un clin d'œil.
• Comparaison Facile : Vous voulez comparer deux fractions ? Encadrer chaque fraction peut vous donner un indice précieux.
• Vérification de Sens : Vous avez fait un calcul avec des fractions ? Encadrer le résultat peut vous aider à vérifier si votre réponse est logique.

Comment Encadrer une Fraction, Pas à Pas

Bon, maintenant qu'on est convaincu de l'utilité de la chose, voyons comment on s'y prend concrètement. C'est beaucoup plus simple qu'il n'y paraît.

L'idée de base, c'est de faire une division. Oui, oui, vous avez bien entendu ! On divise le numérateur (le nombre du haut) par le dénominateur (le nombre du bas). Le quotient (le résultat de la division) sera l'un des nombres entiers qui encadrent la fraction. Et l'entier suivant sera l'autre !

Exemple Concret : 7/3

Prenons l'exemple de la fraction 7/3. On divise 7 par 3 :

7 ÷ 3 = 2 avec un reste de 1.

Le quotient est 2. Cela signifie que 7/3 est plus grand ou égal à 2. Et l'entier suivant, c'est bien sûr 3. Donc, on peut dire que :

2 < 7/3 < 3

On a encadré 7/3 ! C'est comme ça, tout simplement. 7/3 se situe entre 2 et 3. C'est un peu plus que 2, mais pas tout à fait 3.

Autre Exemple : 15/4

Essayons avec 15/4 :

15 ÷ 4 = 3 avec un reste de 3.

Le quotient est 3, donc 15/4 est entre 3 et 4 :

3 < 15/4 < 4

Facile, non ?

Cas Particuliers : Les Fractions Inférieures à 1

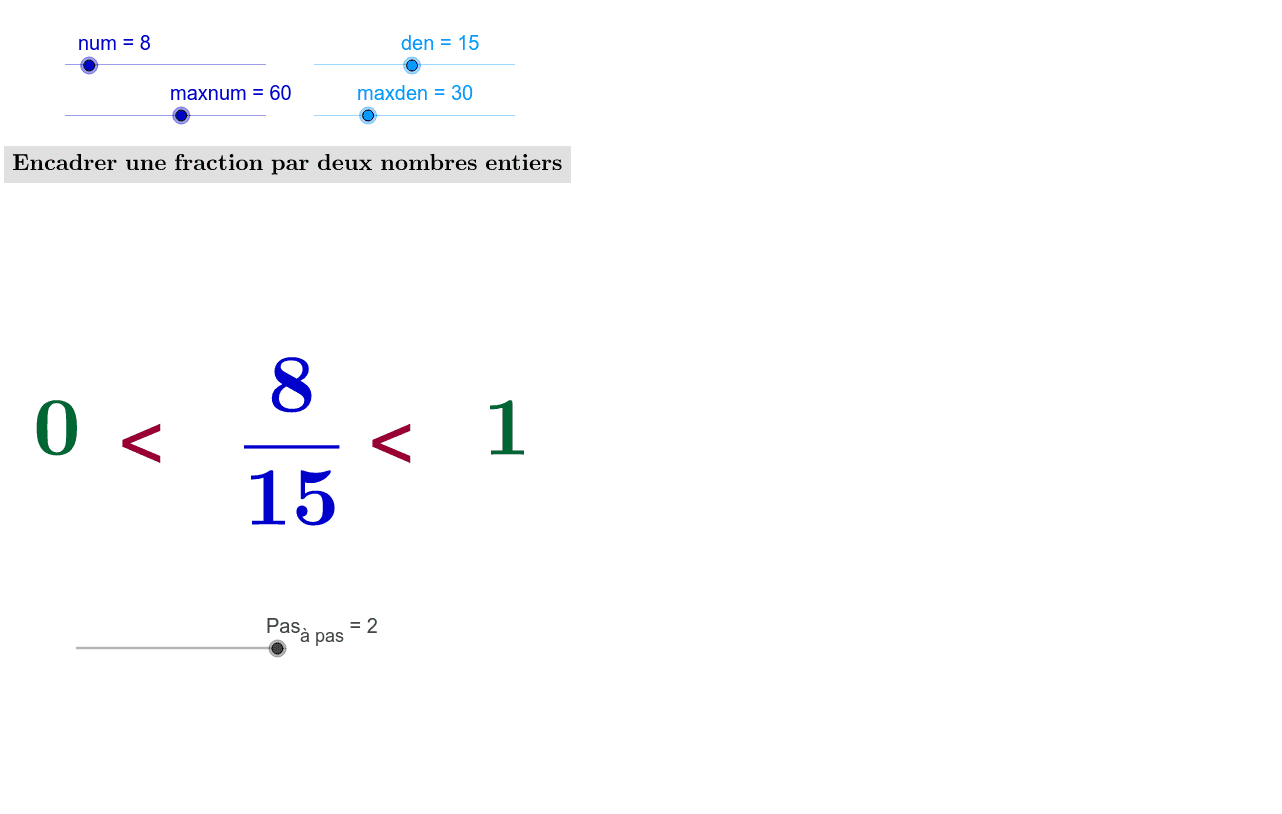
Si vous divisez le numérateur par le dénominateur et que le résultat est inférieur à 1 (par exemple, avec 2/5), cela signifie que la fraction est entre 0 et 1 :

0 < 2/5 < 1

Ces fractions sont plus petites que l'unité.

Pourquoi Ça Marche ? (Un Peu de Théorie)

Ok, c'est bien de savoir faire, mais comprendre *pourquoi* ça marche, c'est encore mieux !

Quand on divise le numérateur par le dénominateur, on cherche à savoir combien de fois le dénominateur "rentre" dans le numérateur. Reprenons l'exemple de 7/3. Quand on divise 7 par 3, on trouve 2 avec un reste de 1. Ça veut dire que 3 "rentre" 2 fois complètement dans 7, et il reste encore un petit bout (le reste, 1). Donc, 7/3 est plus grand que 2 (puisque 3 rentre 2 fois entièrement) et plus petit que 3 (puisqu'il manque encore un bout pour que 3 rentre une troisième fois complètement).

En termes mathématiques, on peut écrire :

7/3 = 2 + 1/3

On voit clairement que 7/3 est égal à 2 entier plus un tiers. C'est donc bien entre 2 et 3.

Petits Trucs et Astuces

• Simplifier la Fraction : Avant de diviser, regardez si vous pouvez simplifier la fraction. Ça peut rendre les calculs plus faciles. Par exemple, 6/8 peut être simplifié en 3/4.
• Fractions Impropres : N'oubliez pas que les fractions impropres (celles où le numérateur est plus grand que le dénominateur) sont toujours supérieures ou égales à 1.
• Utiliser une Calculatrice : Si vous avez des fractions avec des grands nombres, n'hésitez pas à utiliser une calculatrice pour effectuer la division. Le but est de comprendre le concept, pas de devenir un as du calcul mental !

Encadrer, C'est Utile Partout !

L'encadrement de fractions, c'est bien plus qu'une astuce mathématique. Ça nous aide à développer notre sens des nombres et notre capacité à estimer des quantités. Que ce soit pour cuisiner, pour bricoler, ou simplement pour comprendre le monde qui nous entoure, cette compétence est un vrai atout.

Alors, la prochaine fois que vous croisez une fraction, n'hésitez pas à l'encadrer. Vous serez surpris de voir à quel point ça peut vous aider à la visualiser et à la comprendre ! Et qui sait, peut-être que vous deviendrez le roi ou la reine des estimations dans votre entourage !

Alors, prêt à vous lancer ? À vos fractions, et encadrez !