Exercice Théorème De Pythagore 3ème Avec Correction

Salut les curieux ! On se retrouve aujourd'hui pour parler d'un truc qui vous dit peut-être quelque chose, surtout si vous avez passé quelques années au collège : le théorème de Pythagore. Oui, oui, celui-là même. Mais avant de fuir en courant en vous remémorant des cauchemars mathématiques, restez avec moi ! Je vous promets qu'on va explorer ce théorème de manière relax et ludique, avec quelques exercices de 3ème et leurs corrections pour vous mettre en confiance. Alors, prêt à plonger ?

Pourquoi Pythagore est-il si cool ?

Franchement, pourquoi s'intéresser à un truc aussi vieux que Pythagore ? Parce que, figurez-vous, ce n'est pas juste une formule poussiéreuse qu'on vous fait apprendre par cœur. C'est une clé, une brique fondamentale pour comprendre plein de choses autour de nous. Imaginez :

• Construction : Comment les architectes s'assurent-ils que les murs de votre maison sont bien droits ? Bingo, Pythagore !
• Navigation : Comment les marins déterminent-ils la distance entre deux points sur une carte ? Encore lui !
• Jeux vidéo : Comment votre personnage se déplace-t-il en diagonale dans un jeu ? Vous avez deviné...

Le théorème de Pythagore est un peu comme l'alphabet : simple en apparence, mais incroyablement puissant une fois qu'on le maîtrise. C'est la base de plein de choses ! C'est un peu comme apprendre à faire du vélo : une fois que vous savez, vous ne l'oubliez plus jamais, et vous pouvez aller explorer plein de nouveaux horizons.

Le Théorème, en gros (sans prise de tête)

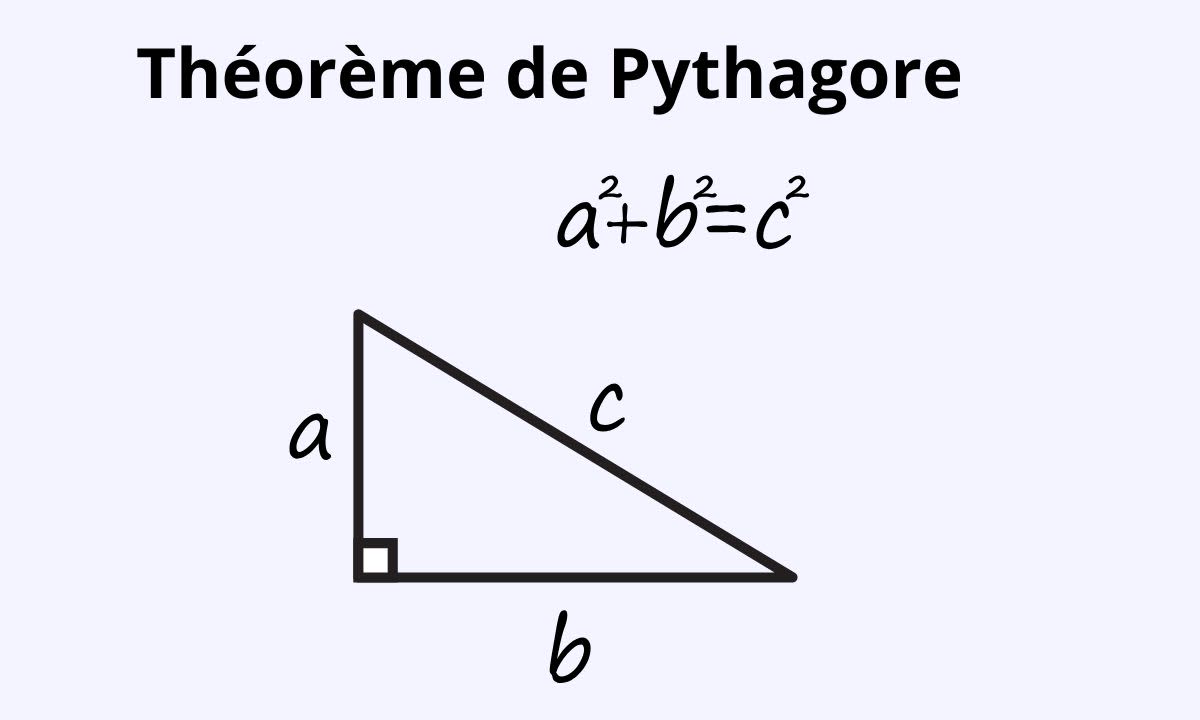
Ok, soyons clairs. Le théorème de Pythagore, qu'est-ce que c'est exactement ? C'est une relation magique qui relie les côtés d'un triangle rectangle. Rappelez-vous, un triangle rectangle, c'est un triangle qui a un angle droit (un angle à 90 degrés, comme le coin d'une feuille de papier). Le côté opposé à l'angle droit, le plus long du triangle, s'appelle l'hypoténuse. Les deux autres côtés s'appellent les côtés adjacents à l'angle droit, souvent appelés simplement "côtés".

La formule, la fameuse, c'est :

a² + b² = c²

Où :

• a et b sont les longueurs des deux côtés (ceux qui forment l'angle droit).
• c est la longueur de l'hypoténuse (le côté opposé à l'angle droit).

En gros, ça veut dire que si vous connaissez les longueurs de deux côtés d'un triangle rectangle, vous pouvez calculer la longueur du troisième ! C'est pas génial, ça ? C'est comme avoir un super pouvoir de mesure !

Exercices de 3ème (avec les solutions, promis !)

Maintenant, passons aux choses sérieuses (mais toujours relax, hein !). On va faire quelques exercices typiques qu'on vous donne en 3ème pour vous aider à bien comprendre comment ça marche. Et surtout, on va regarder les corrections ensemble pour que vous puissiez voir où vous pourriez bloquer.

Exercice 1 : Le classique

On a un triangle rectangle ABC, rectangle en B. AB = 3 cm et BC = 4 cm. Quelle est la longueur de l'hypoténuse AC ?

Solution :

On applique le théorème de Pythagore :

AB² + BC² = AC²

3² + 4² = AC²

9 + 16 = AC²

25 = AC²

Donc, AC = √25 = 5 cm.

Et voilà ! L'hypoténuse mesure 5 cm. C'était facile, non ? C'est comme préparer des pâtes : les ingrédients sont simples, et le résultat est satisfaisant !

Exercice 2 : On se complique un peu la vie (juste un peu !)

On a un triangle rectangle DEF, rectangle en E. DF = 13 cm et DE = 5 cm. Quelle est la longueur de EF ?

Solution :

Attention, piège ! Ici, on connaît l'hypoténuse (DF) et un côté (DE), et on cherche l'autre côté (EF). On applique toujours le théorème, mais on doit le réarranger un peu :

DE² + EF² = DF²

5² + EF² = 13²

25 + EF² = 169

EF² = 169 - 25

EF² = 144

Donc, EF = √144 = 12 cm.

Et hop ! EF mesure 12 cm. Vous voyez, il suffit de bien identifier ce qu'on cherche et ce qu'on connaît. C'est comme déchiffrer un message secret : il faut juste trouver la bonne clé !

Exercice 3 : Le problème concret

Un écran de télévision mesure 80 cm de largeur et 60 cm de hauteur. Quelle est la longueur de sa diagonale ?

Solution :

Ici, la diagonale de l'écran forme l'hypoténuse d'un triangle rectangle dont les côtés sont la largeur et la hauteur de l'écran. On applique Pythagore :

80² + 60² = diagonale²

6400 + 3600 = diagonale²

10000 = diagonale²

Donc, diagonale = √10000 = 100 cm.

La diagonale de l'écran mesure 100 cm (ou 1 mètre). Voilà un exemple concret de l'utilité de Pythagore dans la vie de tous les jours ! C'est un peu comme savoir utiliser une carte : ça vous aide à vous orienter dans le monde réel.

Quelques astuces pour ne plus se tromper

Voici quelques conseils pour éviter les erreurs classiques :

• Bien identifier l'hypoténuse : C'est le côté opposé à l'angle droit, et c'est toujours le plus long.
• Faire attention aux unités : Si les longueurs sont en centimètres, le résultat sera en centimètres aussi.
• Ne pas oublier la racine carrée : À la fin, il faut toujours calculer la racine carrée pour trouver la longueur du côté.
• Vérifier le résultat : Est-ce que la longueur de l'hypoténuse est bien plus grande que les longueurs des deux autres côtés ? Si ce n'est pas le cas, il y a peut-être une erreur.

C'est un peu comme faire une recette de cuisine : suivez les étapes, vérifiez les ingrédients, et vous obtiendrez un résultat délicieux (enfin, un résultat correct, au moins !).

Pythagore, c'est bien plus qu'une formule

J'espère que cet article vous a aidé à dédramatiser le théorème de Pythagore. Ce n'est pas juste une formule à apprendre par cœur, c'est un outil puissant qui peut vous aider à résoudre des problèmes concrets et à mieux comprendre le monde qui vous entoure. Alors, la prochaine fois que vous croiserez un triangle rectangle, pensez à Pythagore et à sa contribution incroyable à la géométrie et à la science en général.

Et n'oubliez pas : la pratique, c'est la clé ! Plus vous ferez d'exercices, plus vous serez à l'aise avec le théorème de Pythagore. Alors, amusez-vous bien et à bientôt pour de nouvelles aventures mathématiques ! C'est un peu comme apprendre une nouvelle langue : plus vous pratiquez, plus vous devenez fluent !

Alors, convaincu que Pythagore, c'est finalement pas si mal ? Et surtout, prêt à relever le défi et à devenir un pro des triangles rectangles ? À vous de jouer !