Exercices Sur La Réciproque Du Théorème De Pythagore

Ah, la réciproque du théorème de Pythagore! Rien que le nom, ça pique un peu, non? On dirait un sortilège que seuls les magiciens des maths peuvent comprendre. Mais détendez-vous, chers amis, point de panique! On va décortiquer ça ensemble, à la cool, avec un peu d'humour et, promis, sans vous faire pleurer. (Enfin, pas trop.)

C'est quoi, ce bazar? Un bref rappel du théorème de base (le "vrai" Pythagore, quoi)

Avant de se lancer dans la réciproque, repassons vite fait les bases. Le théorème de Pythagore, c'est un peu comme la recette de grand-mère pour une tarte aux pommes parfaite : il faut la connaître. Il nous dit que dans un triangle rectangle (celui avec un angle droit, comme un coin de feuille), le carré de la longueur de l'hypoténuse (le côté le plus long, celui qui est en face de l'angle droit) est égal à la somme des carrés des longueurs des deux autres côtés (qu'on appelle les côtés de l'angle droit). En gros :

a² + b² = c²

Où:

a et b sont les longueurs des côtés de l'angle droit.
c est la longueur de l'hypoténuse.

Facile, non? Imaginez un triangle rectangle qui ressemble à une part de pizza. L'hypoténuse, c'est la croûte (la partie la plus appétissante, soyons honnêtes!). Les deux autres côtés, ce sont les bords coupés. Si vous prenez la surface de la croûte au carré (oui, on parle bien de pizza au carré… concept intéressant, à creuser!), c'est la même chose que la somme des surfaces des deux bords coupés au carré. Bon appétit!

La Réciproque: On Inverse la Machine! (Attention, ça tourne!)

Maintenant, accrochez-vous, on passe à la réciproque. La réciproque, c'est un peu comme essayer de remonter le temps. On prend le résultat du théorème (a² + b² = c²) et on se demande : "Si cette équation est vraie, alors est-ce que le triangle est forcément rectangle?" Et la réponse est... oui!

En gros, la réciproque du théorème de Pythagore nous dit :

Si dans un triangle, le carré de la longueur du côté le plus long est égal à la somme des carrés des longueurs des deux autres côtés, alors ce triangle est rectangle.

C'est comme avoir une recette de gâteau et se demander : "Si j'ai ce gâteau, est-ce que j'ai forcément utilisé cette recette?" Si la recette est infaillible et que le gâteau correspond parfaitement aux proportions, alors oui, vous avez bien utilisé cette recette! (Sauf si vous avez triché et utilisé la recette de votre voisine, mais ça, c'est une autre histoire.)

Comment l'utiliser? (Le guide de l'apprenti détective des triangles)

Alors, comment on utilise cette fameuse réciproque dans la vraie vie (enfin, dans les exercices de maths, quoi)? C'est simple, suivez le guide!

1. Repérer le côté le plus long (le suspect principal!)

La première étape, c'est de trouver le côté le plus long du triangle. C'est lui qui va jouer le rôle de l'hypoténuse potentielle. Imaginez que vous êtes un détective et que ce côté est le suspect principal. Il faut l'examiner attentivement.

2. Calculer le carré du côté le plus long (on sort la calculette!)

Ensuite, on calcule le carré de la longueur de ce côté le plus long. On prend sa longueur et on la multiplie par elle-même. Sortez vos calculettes, c'est le moment de faire chauffer les neurones (ou pas, la calculette fera le boulot!).

3. Calculer la somme des carrés des deux autres côtés (les complices?)

Maintenant, on calcule la somme des carrés des longueurs des deux autres côtés. On calcule le carré de chacun de ces côtés, puis on additionne les résultats. Ce sont les complices potentiels du suspect principal. Il faut vérifier s'ils sont de mèche!

4. Comparer les résultats (le verdict!)

La dernière étape, c'est de comparer les deux résultats que vous avez obtenus. Il y a deux possibilités :

Si les résultats sont égaux : Bingo! Le triangle est rectangle! Le suspect principal (le côté le plus long) est bien l'hypoténuse, et les deux autres côtés sont les côtés de l'angle droit. Vous pouvez crier victoire! (Mais pas trop fort, il y a peut-être d'autres exercices à faire.)
Si les résultats sont différents : Dommage! Le triangle n'est pas rectangle. Le suspect principal est innocent, et les deux autres côtés ne sont pas ses complices. Il faut chercher ailleurs! (Ou plus simplement, passer à l'exercice suivant.)

Exemples Concrets (Parce que c'est toujours plus clair avec des chiffres)

Rien de tel que quelques exemples pour illustrer tout ça. Accrochez-vous, on va faire des maths! (Mais promis, ça ne durera pas trop longtemps.)

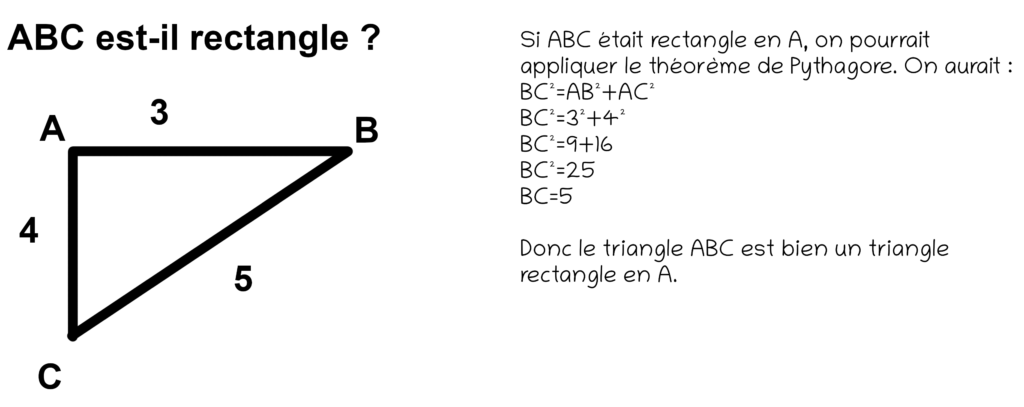
Exemple 1 : Le triangle 3-4-5 (le classique!)

On a un triangle dont les côtés mesurent 3, 4 et 5. Est-ce un triangle rectangle?

Le côté le plus long est 5.
5² = 25
3² + 4² = 9 + 16 = 25
25 = 25

Verdict : Oui, le triangle est rectangle! C'est le fameux triangle 3-4-5, un grand classique des exercices de Pythagore. Il est un peu comme la petite robe noire des maths : il va avec tout!

Exemple 2 : Le triangle 2-3-4 (le rebelle!)

On a un triangle dont les côtés mesurent 2, 3 et 4. Est-ce un triangle rectangle?

Le côté le plus long est 4.
4² = 16
2² + 3² = 4 + 9 = 13
16 ≠ 13

Verdict : Non, le triangle n'est pas rectangle! Il est un peu comme le mouton noir de la famille Pythagore : il ne respecte pas les règles. Il est rebelle, il est différent, il est… non-rectangle! (Bon, on s'emballe peut-être un peu.)

Exemple 3 : Un triangle avec des racines carrées (pour pimenter un peu!)

On a un triangle dont les côtés mesurent √2, √3 et √5. Est-ce un triangle rectangle?

Le côté le plus long est √5.
(√5)² = 5
(√2)² + (√3)² = 2 + 3 = 5
5 = 5

Verdict : Oui, le triangle est rectangle! Même avec des racines carrées, Pythagore ne se laisse pas intimider! C'est un peu comme un chef étoilé qui réussit à faire un plat délicieux avec des ingrédients improbables. Chapeau!

Les pièges à éviter (Attention, zone dangereuse!)

Comme dans tout bon exercice de maths, il y a des pièges à éviter. Voici quelques-uns des plus courants :

Oublier de calculer les carrés : C'est la base! Si vous oubliez de mettre les longueurs au carré, vous êtes sûr de vous tromper. C'est comme essayer de faire une tarte aux pommes sans pommes : ça ne marchera pas!
Se tromper dans les calculs : Une erreur de calcul, ça arrive à tout le monde. Mais il faut essayer de les éviter, sinon vous risquez de conclure que le triangle est rectangle alors qu'il ne l'est pas, ou inversement. C'est comme confondre le sel et le sucre : ça peut gâcher la recette!
Ne pas identifier correctement le côté le plus long : C'est crucial! Si vous vous trompez de côté le plus long, vous êtes sûr de vous planter. C'est comme essayer de mettre le toit d'une maison à la place des fondations : ça ne tiendra pas!
Penser que tous les triangles sont rectangles : C'est faux! La réciproque du théorème de Pythagore ne s'applique qu'aux triangles rectangles. Si vous essayez de l'appliquer à un triangle quelconque, vous allez droit dans le mur. C'est comme essayer de faire rentrer un carré dans un cercle : ça ne fonctionne pas!

Pourquoi c'est important? (La minute "sérieuse", mais pas trop)

Alors, à quoi ça sert, de savoir si un triangle est rectangle ou pas? Eh bien, ça peut être utile dans plein de situations! Par exemple :

En architecture : Pour s'assurer que les angles d'un bâtiment sont droits. Imaginez une maison avec des angles de travers… ça ne serait pas très stable!
En navigation : Pour calculer des distances et des angles. C'est un peu comme avoir un GPS intégré dans votre cerveau (enfin, presque!).
En menuiserie : Pour construire des meubles avec des angles parfaits. Personne ne veut d'une table bancale!
Dans la vie de tous les jours : Pour impressionner vos amis avec vos connaissances en maths. "Tu vois ce triangle? Je peux te dire en un clin d'œil s'il est rectangle ou pas!" Effet garanti!

Un peu d'histoire (Pour briller en société)

Le théorème de Pythagore (et sa réciproque) est attribué à Pythagore, un mathématicien et philosophe grec qui vivait au VIe siècle avant J.-C. Mais en réalité, ce théorème était déjà connu bien avant lui, notamment en Mésopotamie et en Égypte. Pythagore a surtout contribué à sa démonstration rigoureuse et à sa diffusion. C'est un peu comme Christophe Colomb qui a "découvert" l'Amérique : il n'était pas le premier à y mettre les pieds, mais il a contribué à la faire connaître au reste du monde.

La légende raconte que Pythagore était tellement content d'avoir découvert son théorème qu'il a sacrifié cent boeufs aux dieux. C'est un peu excessif, non? On peut se contenter d'une part de pizza pour fêter ça!

Les Applications Avancées (Pour les pros des maths)

Si vous êtes vraiment motivé (ou si votre prof vous l'a demandé!), vous pouvez utiliser la réciproque du théorème de Pythagore pour résoudre des problèmes plus complexes. Par exemple :

Déterminer si un triangle est acutangle (tous les angles sont aigus) ou obtusangle (un angle est obtus) : Si a² + b² > c², le triangle est acutangle. Si a² + b² < c², le triangle est obtusangle. C'est un peu comme deviner le caractère d'une personne en regardant sa photo : il faut être un peu Sherlock Holmes!
Calculer la hauteur d'un triangle : En utilisant la réciproque et d'autres théorèmes, on peut calculer la hauteur d'un triangle à partir de la longueur de ses côtés. C'est un peu comme construire un pont : il faut connaître les mesures exactes pour que ça tienne!

Exercices d'entraînement (Pour devenir un Jedi de Pythagore)

Pour maîtriser la réciproque du théorème de Pythagore, il faut s'entraîner! Voici quelques exercices pour vous mettre au défi :

Un triangle a des côtés de longueur 6, 8 et 10. Est-il rectangle?
Un triangle a des côtés de longueur 5, 12 et 13. Est-il rectangle?
Un triangle a des côtés de longueur 7, 9 et 11. Est-il rectangle?
Un triangle a des côtés de longueur √7, √11 et √18. Est-il rectangle?
Un triangle a des côtés de longueur 2.5, 6 et 6.5. Est-il rectangle?

N'hésitez pas à faire d'autres exercices, à consulter des ressources en ligne, ou à demander de l'aide à votre prof. Plus vous vous entraînerez, plus vous deviendrez un Jedi de Pythagore! (Et moins vous aurez peur des exercices de maths.)

Les ressources en ligne (Pour ne jamais être seul face à Pythagore)

Si vous avez besoin d'aide pour comprendre ou pour vous entraîner, il existe plein de ressources en ligne :

Des sites web de maths : Ils proposent des cours, des exercices, des vidéos, etc. C'est un peu comme avoir un prof particulier à disposition 24h/24!
Des forums de maths : Vous pouvez poser des questions et obtenir des réponses d'autres élèves ou de profs. C'est un peu comme une salle de classe virtuelle!
Des vidéos sur YouTube : Il y a plein de vidéos qui expliquent le théorème de Pythagore et sa réciproque de manière claire et ludique. C'est un peu comme regarder un film sur les maths! (Bon, d'accord, c'est peut-être moins excitant qu'un film d'action, mais ça peut être utile!)
Des applications pour smartphone : Il existe des applications qui vous permettent de vous entraîner, de vérifier vos réponses, etc. C'est un peu comme avoir un coach de maths dans votre poche!

La conclusion (le mot de la fin, enfin!)

Voilà, on a fait le tour de la réciproque du théorème de Pythagore. J'espère que vous avez trouvé ça un peu moins effrayant qu'au début. N'oubliez pas : les maths, c'est comme le vélo, plus on s'entraîne, plus on est à l'aise. Alors, n'hésitez pas à enfourcher votre calculette et à vous lancer à la conquête des triangles rectangles! Et si jamais vous vous perdez, souvenez-vous : a² + b² = c², c'est votre boussole!

Maintenant, si vous excusez, j'ai une envie soudaine de commander une pizza... au carré, bien sûr! Après tout, il faut bien fêter cette victoire mathématique! Et vous, vous faites quoi? Vous allez enfin pouvoir dormir sur vos deux oreilles en sachant que vous maîtrisez la réciproque du théorème de Pythagore? Ou vous allez plutôt vérifier si votre table basse est bien rectangulaire? (Je ne vous juge pas, promis!)

Allez, à la prochaine pour de nouvelles aventures mathématiques! (Et n'oubliez pas, les maths, c'est comme l'amour : il faut s'y donner à fond… ou presque! 😉)