Formula For The Variance

Salut l'ami(e) ! Alors, tu veux qu'on parle de la variance ? Oui, oui, la variance. Ça sonne peut-être un peu intimidant, comme un méchant dans un film de super-héros, mais promis, c'est beaucoup plus simple (et moins dangereux !) que ça en a l'air. Imagine, c'est juste une façon élégante de mesurer à quel point les chiffres dans un ensemble de données sont éparpillés. Pense à une poignée de confetti : plus ils sont dispersés, plus la variance est grande. Facile, non ?
Pourquoi se soucier de la variance ?
Bonne question ! Imagine que tu dois choisir entre deux fournisseurs de tomates pour ta pizzeria. Le premier a des tomates dont le poids varie énormément : certaines sont minuscules, d'autres sont énormes. Le deuxième a des tomates dont le poids est beaucoup plus constant. La variance t'aide à comprendre ça ! Si tu veux des pizzas avec une garniture uniforme, tu vas probablement choisir le deuxième fournisseur, non ? La variance, c'est un peu comme un détecteur d'irrégularités. Et qui n'aime pas détecter les irrégularités ? (Sauf peut-être les irrégularités dans le code, là, c'est moins drôle...).
La formule, décomposée (et sans panique !)
Ok, ok, on y arrive. Je sais que le mot "formule" peut faire peur, mais respire un grand coup ! On va la décortiquer ensemble, étape par étape, et promis, il n'y aura pas de pièges (enfin, peut-être juste un ou deux petits jeux de mots, je n'y peux rien !). La formule de la variance (pour un échantillon, attention !) est :
s² = Σ (xi - x̄)² / (n - 1)
Alors, on dirait du hiéroglyphe, mais en réalité, c'est juste une suite d'instructions. Voyons ça de plus près :
- s² : C'est la variance ! Oui, oui, c'est tout ce qu'on cherche à calculer. Le petit "²" indique qu'on élève au carré (on verra pourquoi plus tard).
- Σ (Sigma) : C'est le symbole de la somme. Ça veut dire qu'on va additionner plein de trucs ensemble. Imagine que tu additionnes tous les bonbons dans ton sac d'Halloween (sans les manger tout de suite, promis ?).
- xi : C'est chaque valeur dans ton ensemble de données. Par exemple, si tu mesures la taille de cinq personnes, chaque taille est un "xi". Pense à chaque personne comme un pixel dans une photo.
- x̄ (x barre) : C'est la moyenne de tes données. Tu sais, celle qu'on calcule en additionnant toutes les valeurs et en divisant par le nombre de valeurs. C'est un peu comme le point central de ton ensemble de données.
- (xi - x̄) : C'est la différence entre chaque valeur et la moyenne. Ça te dit à quel point chaque valeur s'éloigne du centre. On l'appelle aussi "écart à la moyenne". C'est comme mesurer la distance entre chaque confetti et le milieu de la table.
- (xi - x̄)² : On prend cette différence et on l'élève au carré. Pourquoi ? Parce qu'on ne veut pas que les différences négatives et positives s'annulent ! Si on avait des nombres négatifs et positifs, ils s’annuleraient quand on les additionnerait, ce qui nous donnerait une variance de zéro (ce qui voudrait dire qu'il n'y a pas de variance !). Elever au carré rend tout positif, et ça amplifie aussi les grandes différences, ce qui est bien pour détecter les valeurs extrêmes. C'est comme punir plus sévèrement les confetti qui se sont vraiment éloignés de la table.
- (n - 1) : C'est le nombre de valeurs dans ton échantillon, moins un. Pourquoi "moins un" ? C'est une correction technique qui s'appelle "degré de liberté". On l'utilise quand on calcule la variance d'un échantillon pour estimer la variance de toute la population. Ne t'inquiète pas trop de ça pour l'instant, retiens juste qu'il faut soustraire un ! Pense à ce -1 comme à un petit lutin farceur qui se cache dans la formule.
Un exemple concret (avec des chatons !)
Imagine que tu pèses cinq chatons. Voici leurs poids (en grammes) : 100, 120, 130, 110, 140. On va calculer la variance ensemble !
- Calcule la moyenne (x̄) : (100 + 120 + 130 + 110 + 140) / 5 = 120
- Calcule les écarts à la moyenne (xi - x̄) : -20, -0, 10, -10, 20
- Elève au carré les écarts (xi - x̄)² : 400, 0, 100, 100, 400
- Somme les écarts au carré (Σ (xi - x̄)²) : 400 + 0 + 100 + 100 + 400 = 1000
- Divise par (n - 1) : 1000 / (5 - 1) = 1000 / 4 = 250
La variance du poids des chatons est donc de 250 grammes carrés. Oui, "grammes carrés", l'unité est un peu bizarre, mais c'est juste une conséquence du fait qu'on a élevé au carré les écarts. Pour avoir une idée plus intuitive de la dispersion, on peut calculer l'écart type (standard deviation) qui est la racine carrée de la variance : √250 ≈ 15.8 grammes. Ça veut dire que le poids des chatons varie en moyenne d'environ 15.8 grammes par rapport à la moyenne. Voilà, tu as maintenant une idée de la dispersion des poids de ces adorables chatons!
Variance et population vs. échantillon : Le détail qui change tout !
Attention, petit détail important ! Si au lieu d'avoir un échantillon de chatons, tu avais tous les chatons du monde (chanceux!), tu utiliserais une formule légèrement différente pour la variance. Au lieu de diviser par (n - 1), tu diviserais simplement par n (le nombre total d'éléments dans ta population). La formule deviendrait alors :
σ² = Σ (xi - μ)² / N
Où σ² est la variance de la population, μ est la moyenne de la population, et N est la taille de la population. C'est subtil, mais c'est important de le savoir ! C’est comme la différence entre « c’est » et « ses »; ça change tout !
Les pièges à éviter (ou comment ne pas te prendre les pieds dans le tapis !)
Calculer la variance, ce n'est pas sorcier, mais il y a quelques petits pièges dans lesquels on peut facilement tomber :
- Oublier d'élever au carré ! C'est l'erreur classique. Si tu oublies d'élever au carré les écarts à la moyenne, tu vas te retrouver avec une variance fausse (et probablement nulle, ce qui est encore plus trompeur !).
- Mélanger les populations et les échantillons ! N'oublie pas la différence entre diviser par n et diviser par (n - 1). Ça peut faire une différence significative, surtout si ton échantillon est petit.
- Ne pas vérifier tes calculs ! Surtout si tu fais les calculs à la main, c'est toujours une bonne idée de vérifier tes résultats avec une calculatrice ou un logiciel statistique.
- Paniquer ! La variance, c'est juste un outil. Si tu te trompes, ce n'est pas grave. Relis la formule, vérifie tes calculs, et tout ira bien. (Et si tu paniques vraiment, offre-toi un morceau de chocolat. Ça aide toujours !)
En conclusion (et avec le sourire !)
Voilà, tu sais maintenant tout (ou presque !) sur la variance. Tu as vu que ce n'est pas si compliqué que ça en a l'air, et que c'est même un outil super utile pour comprendre la dispersion de tes données. Alors, la prochaine fois que tu entendras parler de variance, ne t'enfuis pas en courant ! Au contraire, souris, et dis-toi que tu sais exactement de quoi il s'agit. Tu es désormais un(e) maître(sse) de la variance, un(e) véritable détective des données ! Et si jamais tu as un doute, reviens lire cet article. Je serai toujours là pour te rappeler que les statistiques, c'est avant tout une question de logique... et un peu d'humour ! Alors, à toi les joies de l'analyse de données! N'aie pas peur d'être bizarre; aie peur d'être le même que tout le monde!
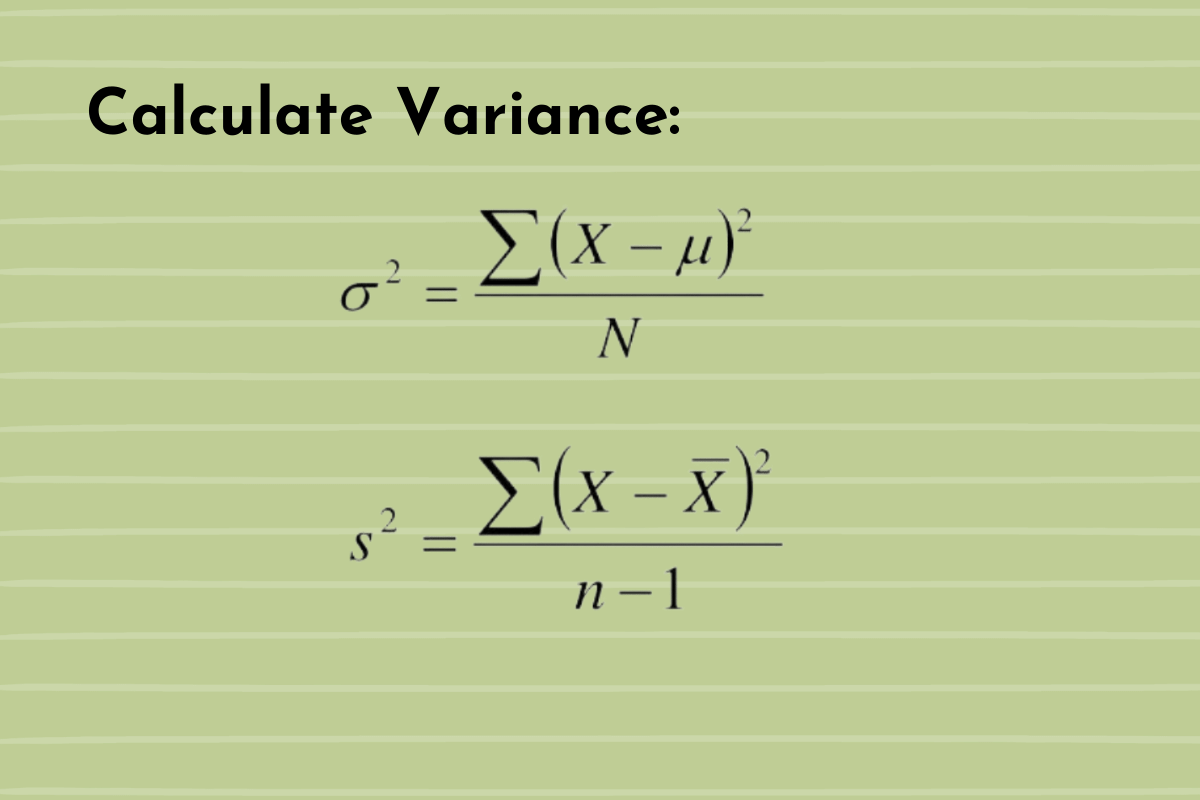



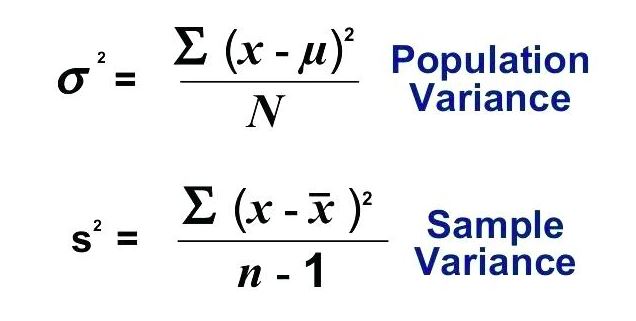






:max_bytes(150000):strip_icc()/latex_104ab167efe3f6e76039876d42dfde0e-5c5b1b7746e0fb00017dcf53.jpg)






