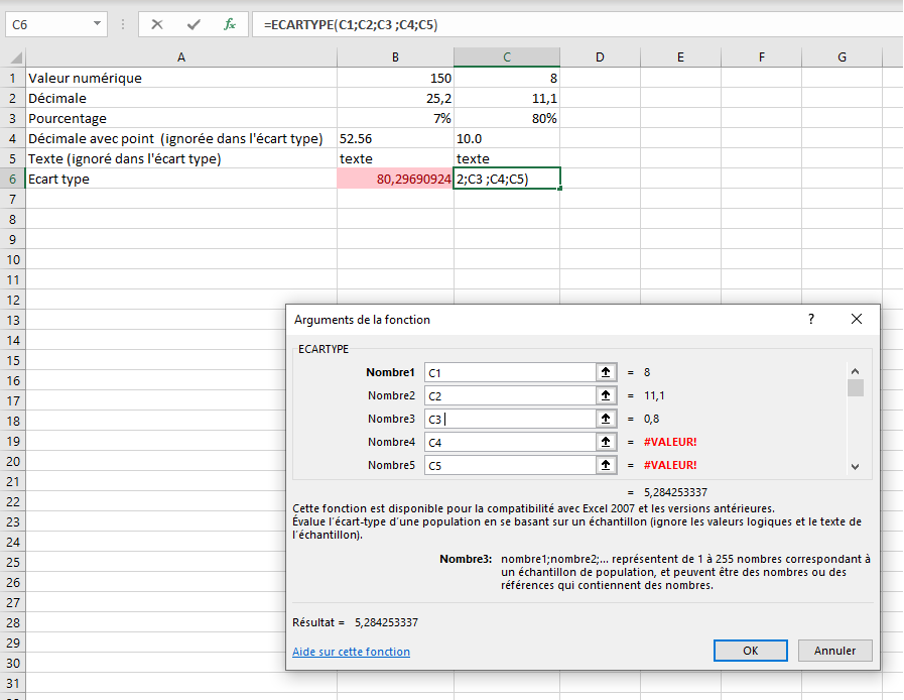
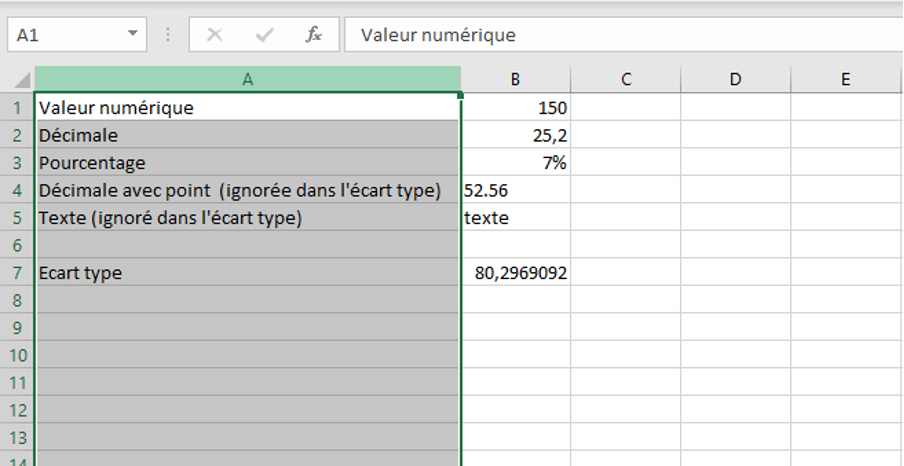
Formule Calcul écart Type

Ah, l'écart type! Rien que le nom, ça sonne déjà comme une punition de maths. Mais promis, après cette petite explication, vous ne le verrez plus comme un monstre caché sous votre lit. On va décortiquer cette bête ensemble, sans prise de tête, et je vais même essayer de vous faire sourire au passage. Accrochez-vous!

C'est quoi, ce truc, en fait?

Imaginez une bande d'amis qui décident de jouer au bowling. Certains sont des pros, ils font des strikes à chaque lancer. D'autres... disons qu'ils sont plus doués pour encourager les autres (et boire des bières). L'écart type, c'est un peu comme une mesure de la dispersion de leurs scores. Si tous les scores sont proches les uns des autres (tout le monde fait entre 6 et 8 quilles), l'écart type est petit. Si les scores sont hyper différents (un strike, une gouttière, un 7, un 2...), alors l'écart type est grand. En gros, ça nous dit à quel point les données sont regroupées ou éparpillées.

Pensez à une classe d'élèves. Si tous ont entre 12 et 14 de moyenne, l'écart type est faible. Par contre, si certains explosent le plafond avec des 18, et d'autres galèrent avec des 8, l'écart type grimpe en flèche! C'est un indicateur de l'hétérogénéité du groupe.

La Formule (Sans Paniquer!)

Ok, on y arrive. La fameuse formule. Ne fuyez pas! Je vais la simplifier au maximum. La formule de l'écart type, c'est un peu comme une recette de cuisine. Il faut suivre les étapes, et même si on ne comprend pas toujours pourquoi on fait ça, à la fin, on obtient un résultat.

Elle se décompose en quelques étapes clés:

1. Calculer la moyenne : C'est la somme de toutes les valeurs, divisée par le nombre de valeurs. Facile! Si nos scores au bowling sont 5, 7, 9, 6 et 8, la moyenne est (5+7+9+6+8) / 5 = 7.
2. Calculer les écarts à la moyenne : Pour chaque valeur, on calcule la différence entre cette valeur et la moyenne. Dans notre exemple : 5-7=-2, 7-7=0, 9-7=2, 6-7=-1, 8-7=1.
3. Élever les écarts au carré : On prend chaque écart et on le multiplie par lui-même. Pourquoi? Pour se débarrasser des nombres négatifs et donner plus de poids aux grandes différences. Ça donne : (-2)²=4, 0²=0, 2²=4, (-1)²=1, 1²=1.
4. Calculer la moyenne des carrés des écarts : On additionne tous les résultats de l'étape précédente, et on divise par le nombre de valeurs. C'est la variance! Dans notre cas : (4+0+4+1+1) / 5 = 2.
5. Prendre la racine carrée : On calcule la racine carrée du résultat précédent. Et voilà, l'écart type est là! √2 ≈ 1.41.

Bon, je sais, ça paraît barbare écrit comme ça. Mais si vous suivez les étapes une par une, avec un petit exemple concret, vous verrez que ce n'est pas si compliqué. Et puis, il existe des calculateurs en ligne qui font tout le boulot à votre place. L'important, c'est de comprendre l'idée générale.

Pourquoi on s'embête avec ça?

C'est une excellente question! L'écart type, c'est un outil super pratique dans plein de domaines. Voici quelques exemples :

• Finance : Pour évaluer le risque d'un investissement. Un investissement avec un écart type élevé est plus risqué, car ses rendements varient beaucoup. Imaginez deux actions : une dont le cours fluctue énormément (genre, elle monte de 20% un jour, puis perd 15% le lendemain), et une autre dont le cours est plus stable. L'action volatile aura un écart type élevé, ce qui indique un risque plus important.
• Sciences : Pour analyser des données expérimentales. On l'utilise par exemple pour vérifier si les résultats d'une expérience sont cohérents.
• Marketing : Pour comprendre le comportement des consommateurs. Est-ce que tous les clients réagissent de la même manière à une publicité? Ou y a-t-il de grandes différences?
• Sports : Pour évaluer la performance des athlètes. Un joueur de basket régulier aura un écart type faible concernant le nombre de points qu'il marque par match, tandis qu'un joueur plus irrégulier aura un écart type plus élevé.

En fait, l'écart type est utile dès qu'on a besoin de comparer des ensembles de données et de comprendre leur variabilité. C'est un peu comme avoir une loupe pour examiner les détails d'une image.

L'écart type et la loi normale : Un Duo de Choc

Si vous avez déjà entendu parler de la loi normale (ou courbe de Gauss, cette fameuse courbe en cloche), sachez que l'écart type est son meilleur ami. La loi normale décrit la distribution de nombreuses données (taille des gens, notes à un examen, etc.). L'écart type nous dit à quel point la courbe est étalée ou resserrée. Un petit écart type signifie une courbe resserrée autour de la moyenne, tandis qu'un grand écart type signifie une courbe plus étalée.

Imaginez une épreuve de lancer de fléchettes. Si tous les joueurs sont des pros, leurs fléchettes atterriront toutes très près du centre de la cible. La distribution des impacts suivra une loi normale avec un écart type faible. Par contre, si les joueurs sont des débutants, les fléchettes seront éparpillées un peu partout sur la cible. La distribution des impacts suivra toujours une loi normale, mais avec un écart type élevé.

Quelques Petits Trucs Pour Mieux Comprendre

• Visualisez : Essayez de représenter les données graphiquement. Un histogramme ou un diagramme en boîte peuvent vous aider à voir la dispersion.
• Comparez : Calculez l'écart type de différents ensembles de données et comparez-les. Ça vous donnera une idée de la variabilité relative.
• Utilisez des outils : Ne vous cassez pas la tête à faire les calculs à la main. Il existe plein de logiciels et de calculateurs en ligne qui peuvent vous aider.
• Entrainez-vous : Plus vous utiliserez l'écart type, plus vous vous familiariserez avec lui. Prenez des exemples concrets et amusez-vous à calculer l'écart type.

En résumé, l'écart type n'est pas aussi effrayant qu'il en a l'air. C'est un outil puissant qui peut vous aider à comprendre la variabilité des données et à prendre des décisions éclairées. Alors, la prochaine fois que vous entendrez parler d'écart type, ne fuyez pas! Souvenez-vous de nos amis les joueurs de bowling, et vous verrez que ce n'est pas si compliqué que ça.

Et surtout, n'oubliez pas : les maths, c'est comme le vélo. Au début, on a l'impression qu'on va tomber à chaque instant. Mais une fois qu'on a compris le truc, on peut aller partout!