Formule De L écart Type

Salut toi ! Oui, toi qui lis cet article ! T'es-tu déjà demandé comment on pouvait mesurer la dispersion d'un ensemble de données ? Non ? Eh bien, prépare-toi, car on va plonger ensemble dans le monde fascinant (et oui, je dis bien fascinant !) de la formule de l'écart type. Accroche-toi, ça va décoiffer, mais promis, à la fin, tu te sentiras comme un vrai pro des statistiques !

L'écart type, c'est quoi en fait ?

Imagine, tu as deux équipes de basket. L'équipe A marque en moyenne 70 points par match, et l'équipe B aussi ! Mais si je te dis que l'équipe A marque toujours entre 68 et 72 points, alors que l'équipe B marque parfois 40 points et d'autres fois 100, tu vois bien qu'il y a une différence, non ? C'est là que l'écart type entre en jeu. Il nous dit à quel point les scores sont éparpillés autour de la moyenne.

En gros, l'écart type, c'est un peu comme la météo des données. Si l'écart type est faible, c'est le beau temps, les données sont regroupées et prévisibles. Si l'écart type est élevé, c'est la tempête, les données sont dispersées et imprévisibles ! Tu commences à comprendre ? Super !

La formule, parlons-en ! (Pas de panique !)

Bon, je sais, dès qu'on parle de formule, ça peut faire peur. Mais crois-moi, c'est beaucoup plus simple qu'il n'y paraît. La formule de l'écart type, la voilà :

σ = √[ Σ (xi - μ)² / N ]

"Oulala, c'est quoi tous ces symboles barbares ?" Pas de panique, on va décortiquer ça ensemble, étape par étape, comme si on préparait une délicieuse crêpe !

• σ (sigma) : C'est l'écart type lui-même. C'est lui qu'on cherche à calculer, notre Graal statistique !
• Σ (sigma majuscule) : C'est le symbole de la somme. Ça veut dire qu'on va additionner plusieurs choses ensemble. Facile, non ?
• xi : Ce sont tes données individuelles. Par exemple, si tu mesures la taille de tes amis, xi ce serait la taille de chacun d'eux.
• μ (mu) : C'est la moyenne de tes données. Pour la calculer, tu additionnes toutes tes données et tu divises par le nombre de données. Tu te souviens de ça de l'école primaire ?
• N : C'est le nombre total de données que tu as. Si tu as mesuré la taille de 10 amis, N = 10.
• √ : C'est la racine carrée. On l'utilise à la fin pour obtenir l'écart type dans la bonne unité.

Alors, c'est plus clair maintenant ? On dirait une recette de cuisine !

Exemple concret : Calculons l'écart type !

Prenons un exemple simple. Imaginons que tu veuilles connaître l'écart type des notes que tu as obtenues à tes 5 derniers examens : 12, 14, 15, 16, 18.

1. Calcul de la moyenne (μ) : (12 + 14 + 15 + 16 + 18) / 5 = 15
2. Calcul des écarts à la moyenne (xi - μ) :
   • 12 - 15 = -3
   • 14 - 15 = -1
   • 15 - 15 = 0
   • 16 - 15 = 1
   • 18 - 15 = 3
3. Calcul des écarts au carré (xi - μ)² :
   • (-3)² = 9
   • (-1)² = 1
   • (0)² = 0
   • (1)² = 1
   • (3)² = 9
4. Somme des écarts au carré (Σ (xi - μ)²) : 9 + 1 + 0 + 1 + 9 = 20
5. Division par le nombre de données (Σ (xi - μ)² / N) : 20 / 5 = 4
6. Racine carrée (√[ Σ (xi - μ)² / N ]) : √4 = 2

Tadaaa ! L'écart type de tes notes est de 2. Ça veut dire que tes notes sont relativement regroupées autour de la moyenne de 15. Tu vois, ce n'est pas si sorcier !

Pourquoi l'écart type, c'est génial ?

Maintenant que tu sais calculer l'écart type (bravo !), tu te demandes peut-être à quoi ça sert concrètement. Eh bien, les applications sont innombrables !

• Finance : Pour mesurer le risque d'un investissement. Un investissement avec un écart type élevé est plus risqué qu'un investissement avec un écart type faible.
• Science : Pour analyser les résultats d'une expérience et vérifier si les données sont fiables.
• Marketing : Pour comprendre les préférences des consommateurs et cibler les campagnes publicitaires.
• Sport : Pour évaluer la performance des athlètes et identifier les domaines à améliorer.
• Dans la vie de tous les jours : Pour comparer des ensembles de données, prendre des décisions éclairées et comprendre le monde qui nous entoure ! Par exemple, tu peux comparer la régularité de deux lignes de bus pour choisir celle qui arrive à l'heure !

En fait, l'écart type est un outil puissant qui peut t'aider à comprendre et à analyser n'importe quel type de données. C'est un peu comme avoir une loupe pour observer le monde avec plus de précision !

L'écart type et les logiciels statistiques

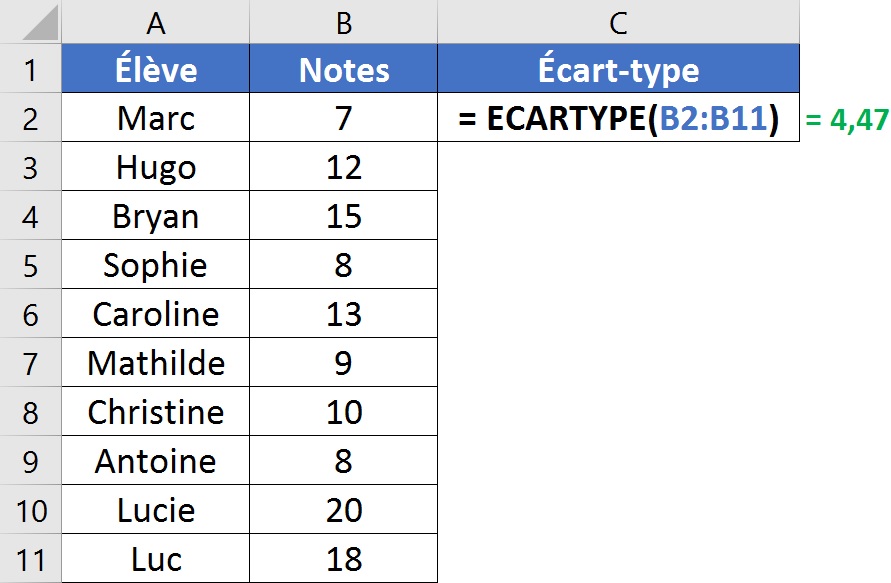
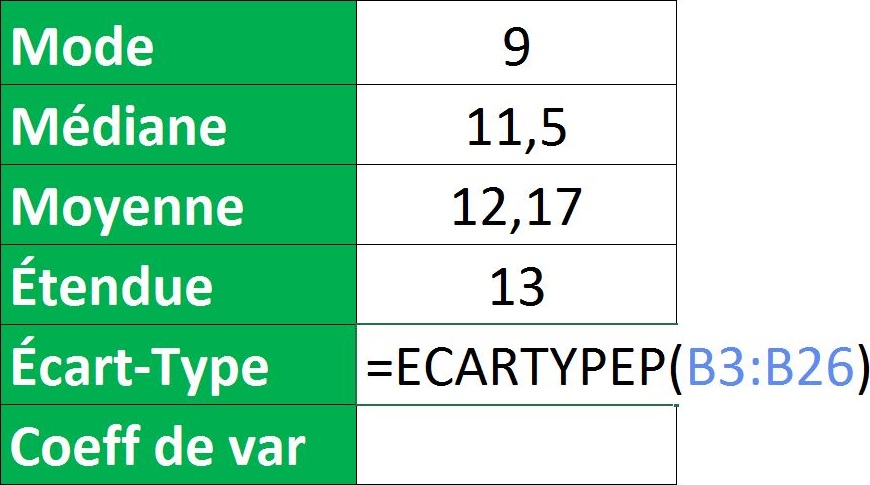
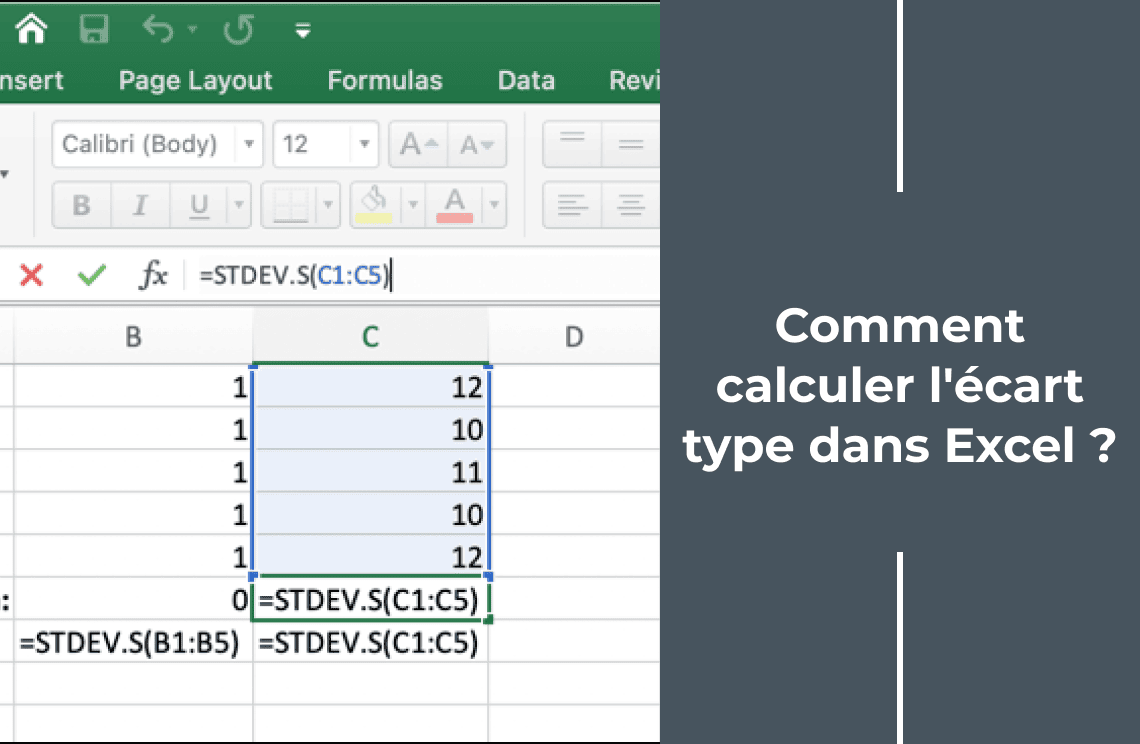
Soyons honnêtes, personne ne calcule l'écart type à la main tous les jours. Heureusement, il existe de nombreux logiciels statistiques (comme Excel, R, Python, etc.) qui peuvent le faire pour toi en un clin d'œil. Ces outils te permettent de te concentrer sur l'interprétation des résultats plutôt que sur les calculs fastidieux.

Apprendre à utiliser ces logiciels est un excellent moyen de booster tes compétences en analyse de données. Et crois-moi, c'est une compétence très recherchée dans le monde professionnel !

Alors, prêt à devenir un expert de l'écart type ?

J'espère que cet article t'a donné envie d'en savoir plus sur l'écart type. C'est un concept simple mais puissant qui peut t'aider à comprendre le monde qui t'entoure. Alors n'hésite pas à explorer, à expérimenter, et à te lancer dans l'aventure des statistiques !

N'aie pas peur des chiffres, ils sont tes amis ! Ils peuvent t'aider à prendre de meilleures décisions, à résoudre des problèmes complexes et à voir le monde sous un angle nouveau. Alors, ouvre ton esprit, saisis ta calculatrice (ou ton logiciel statistique préféré) et pars à la découverte de la magie des données ! L'aventure ne fait que commencer !

Et n'oublie pas, l'apprentissage est un voyage, pas une destination. Alors amuse-toi, explore, et n'aie pas peur de te tromper. C'est en faisant des erreurs qu'on apprend le plus ! Bon courage et à bientôt pour de nouvelles aventures statistiques !