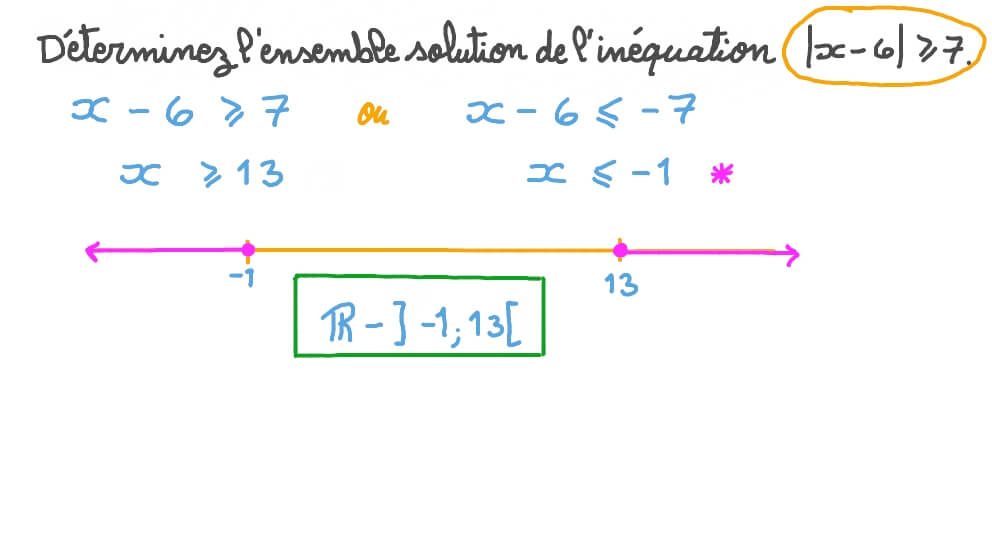Résoudre Une Inéquation Supérieur Ou égal à 0

Salut l'ami ! Tu t'es déjà demandé comment vraiment maîtriser une compétence qui te semble un peu... intimidante ? Aujourd'hui, on va déchiffrer ensemble un truc qui peut sembler barbare au premier abord : résoudre une inéquation supérieure ou égale à 0. Accroche-toi, promis, ça va être plus fun que tu ne le penses ! On va transformer ce qui te semble être un défi en une aventure passionnante. (Oui, oui, je sais, les maths et l'aventure, ça peut surprendre, mais fais-moi confiance !)

Pourquoi s'embêter avec les inéquations ?

Bonne question ! Pourquoi passer du temps sur ça alors qu'il y a Netflix, des jeux vidéo, et des tas d'autres choses bien plus divertissantes ? Eh bien, la réponse est simple : résoudre une inéquation, c'est un peu comme débloquer un super pouvoir !

Imagine que tu dois prendre une décision importante : investir dans un nouveau projet, organiser un événement, ou même choisir quel parfum de glace tu vas prendre (crucial, on est d'accord !). Les inéquations t'aident à définir les conditions pour que ton projet réussisse, que ton événement soit un succès, ou que... bon, tu aies la meilleure glace possible !

Plus concrètement, ça te permet de comprendre quand une quantité est positive, c'est-à-dire supérieure ou égale à zéro. Et devine quoi ? Être positif, c'est souvent une bonne chose, que ce soit en maths ou dans la vie ! (Clin d'œil)

Le B.A.-BA : Qu'est-ce qu'une inéquation ?

Alors, concrètement, une inéquation, c'est comme une équation... mais avec un petit twist ! Au lieu d'avoir un signe "égal" (=), on a un signe d'inégalité. Par exemple :

* x + 2 > 0 (x plus 2 est supérieur à 0) * 3x - 5 ≥ 0 (3x moins 5 est supérieur ou égal à 0)

Le but du jeu, c'est de trouver toutes les valeurs de 'x' qui rendent l'inégalité vraie. C'est un peu comme chercher le mot de passe qui déverrouille un coffre rempli de connaissances et de possibilités !

Comment résoudre une inéquation du premier degré ?

On commence en douceur, avec les inéquations du premier degré, c'est-à-dire celles où 'x' est à la puissance 1 (pas de x², x³, etc.). La méthode est super simple :

Isoler 'x' : On fait exactement comme pour une équation : on déplace les termes de chaque côté de l'inégalité pour avoir 'x' tout seul d'un côté. Attention, il y a une petite règle d'or à connaître...
La règle d'or de la multiplication/division par un nombre négatif : Si tu multiplies ou divises les deux côtés de l'inéquation par un nombre négatif, tu dois inverser le sens de l'inégalité ! C'est le petit piège à éviter.
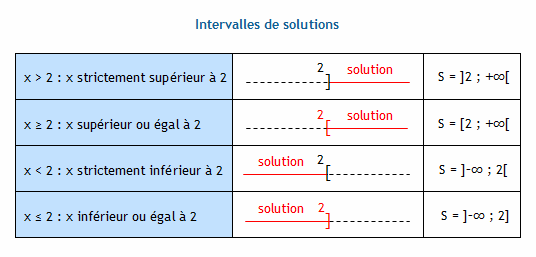
Exprimer la solution : On écrit la solution sous forme d'intervalle. Par exemple, si on trouve x ≥ 3, la solution est [3, +∞[. (Le crochet signifie "inclus", la parenthèse signifie "exclu").

Exemple concret :

Résolvons l'inéquation 2x - 4 ≥ 0.

On ajoute 4 des deux côtés : 2x ≥ 4
On divise par 2 : x ≥ 2
La solution est donc [2, +∞[. Ça veut dire que toutes les valeurs de 'x' supérieures ou égales à 2 vérifient l'inéquation !

Facile, non ? (Bon, peut-être pas du premier coup, mais avec un peu de pratique, ça vient tout seul !)

Et les inéquations du second degré ?

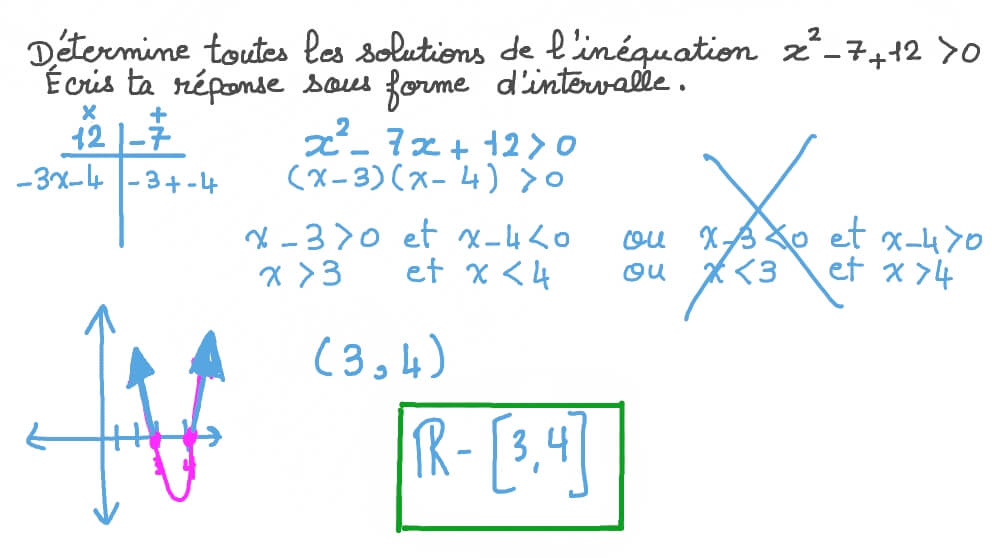
Ça se corse un peu, mais pas de panique ! Les inéquations du second degré (celles avec du x²) demandent une petite gymnastique supplémentaire. Voici les étapes clés :

Mettre l'inéquation sous la forme ax² + bx + c ≥ 0 : On s'assure que tout est du même côté de l'inégalité et qu'on a zéro de l'autre côté.
Trouver les racines du polynôme ax² + bx + c : On résout l'équation ax² + bx + c = 0. On peut utiliser la formule du discriminant (Δ = b² - 4ac) ou, si on est chanceux, trouver les racines "à l'œil".
Faire un tableau de signes : C'est là que la magie opère ! On trace un tableau avec une ligne pour 'x', une ligne pour (x - racine1), une ligne pour (x - racine2), et une ligne pour ax² + bx + c. On met les racines dans l'ordre croissant sur la ligne 'x'. Ensuite, on remplit le tableau avec les signes "+" et "-" en fonction de la position de 'x' par rapport aux racines.
Déterminer les intervalles où ax² + bx + c ≥ 0 : On regarde les lignes du tableau et on identifie les intervalles où le polynôme est positif ou nul. Ce sont ces intervalles qui constituent la solution de l'inéquation !

Exemple pour illustrer :

Résolvons l'inéquation x² - 3x + 2 ≥ 0.

On a déjà la bonne forme : x² - 3x + 2 ≥ 0
On trouve les racines de x² - 3x + 2 = 0 : les racines sont 1 et 2. (On peut utiliser la formule du discriminant ou factoriser : (x-1)(x-2) = 0)
On fait le tableau de signes :

        x       | -∞     1     2     +∞
    -------------------------------------
    x - 1     |  -      0     +     +
    x - 2     |  -      -     0     +
    x²-3x+2  |  +      0     -     0    +

On identifie les intervalles où x² - 3x + 2 ≥ 0 : on voit que le polynôme est positif (ou nul) sur ]-∞, 1] et [2, +∞[.
La solution est donc ]-∞, 1] ∪ [2, +∞[. (Le symbole ∪ signifie "union", on combine les deux intervalles).

Un peu plus compliqué, c'est vrai, mais avec le tableau de signes, ça devient beaucoup plus clair. Entraîne-toi, c'est la clé !

Aller plus loin : Inéquations avec des fractions et des valeurs absolues

Si tu te sens l'âme d'un aventurier des maths, tu peux t'attaquer aux inéquations un peu plus corsées, comme celles avec des fractions ou des valeurs absolues. La bonne nouvelle, c'est que les principes de base restent les mêmes !

* Inéquations avec des fractions : On met tout sur le même dénominateur, puis on étudie le signe du numérateur et du dénominateur séparément dans un tableau de signes. Attention aux valeurs interdites (celles qui annulent le dénominateur) ! * Inéquations avec des valeurs absolues : On utilise la définition de la valeur absolue : |x| = x si x ≥ 0, et |x| = -x si x < 0. On doit donc séparer l'inéquation en plusieurs cas, en fonction du signe de l'expression à l'intérieur de la valeur absolue.

Ces types d'inéquations demandent un peu plus de rigueur et de méthode, mais ils sont tout à fait abordables avec de la pratique et de la patience.

Pourquoi c'est important et comment ça peut rendre ta vie meilleure ?

Tu te dis peut-être encore : "Oui, c'est bien joli tout ça, mais à quoi ça me sert vraiment dans la vraie vie ?"

Eh bien, les inéquations, c'est comme un outil de pensée critique super puissant. Ça te permet de :

* Prendre des décisions éclairées : En comprenant les conditions nécessaires pour atteindre un objectif, tu peux prendre des décisions plus judicieuses. * Résoudre des problèmes concrets : Que ce soit pour optimiser un budget, planifier un projet, ou comprendre un phénomène scientifique, les inéquations peuvent t'aider à trouver des solutions. * Développer ton esprit logique : Résoudre des inéquations, c'est un peu comme résoudre des énigmes. Ça stimule ton cerveau et renforce ta capacité à raisonner.

Et puis, soyons honnêtes, la satisfaction de résoudre une inéquation complexe, c'est un peu comme gagner une partie d'échecs : on se sent intelligent, compétent, et prêt à conquérir le monde ! (Bon, peut-être pas le monde entier, mais au moins le prochain chapitre de ton cours de maths !)

Conclusion : Lance-toi !

J'espère que cet article t'a donné envie de te plonger dans le monde fascinant des inéquations. N'aie pas peur de te tromper, c'est en faisant des erreurs qu'on apprend. L'important, c'est de persévérer et de ne jamais abandonner.

Alors, prêt à relever le défi ? Prends un crayon, une feuille de papier, et lance-toi ! Tu verras, résoudre une inéquation, c'est un peu comme ouvrir une porte vers un monde de possibilités. Et qui sait, peut-être que tu découvriras une passion insoupçonnée pour les maths ! (On ne sait jamais...)

Il existe une multitude de ressources en ligne, de livres et de tutoriels pour t'aider dans ton apprentissage. N'hésite pas à explorer, à expérimenter, et à poser des questions. La connaissance est à portée de main, il suffit de la saisir !

Et souviens-toi : même les plus grands mathématiciens ont commencé un jour par apprendre les bases. Alors, pourquoi pas toi ? Allez, fonce !